P12054 [THUPC 2025 决赛] 食堂

……所以为什么会有两道食堂题？

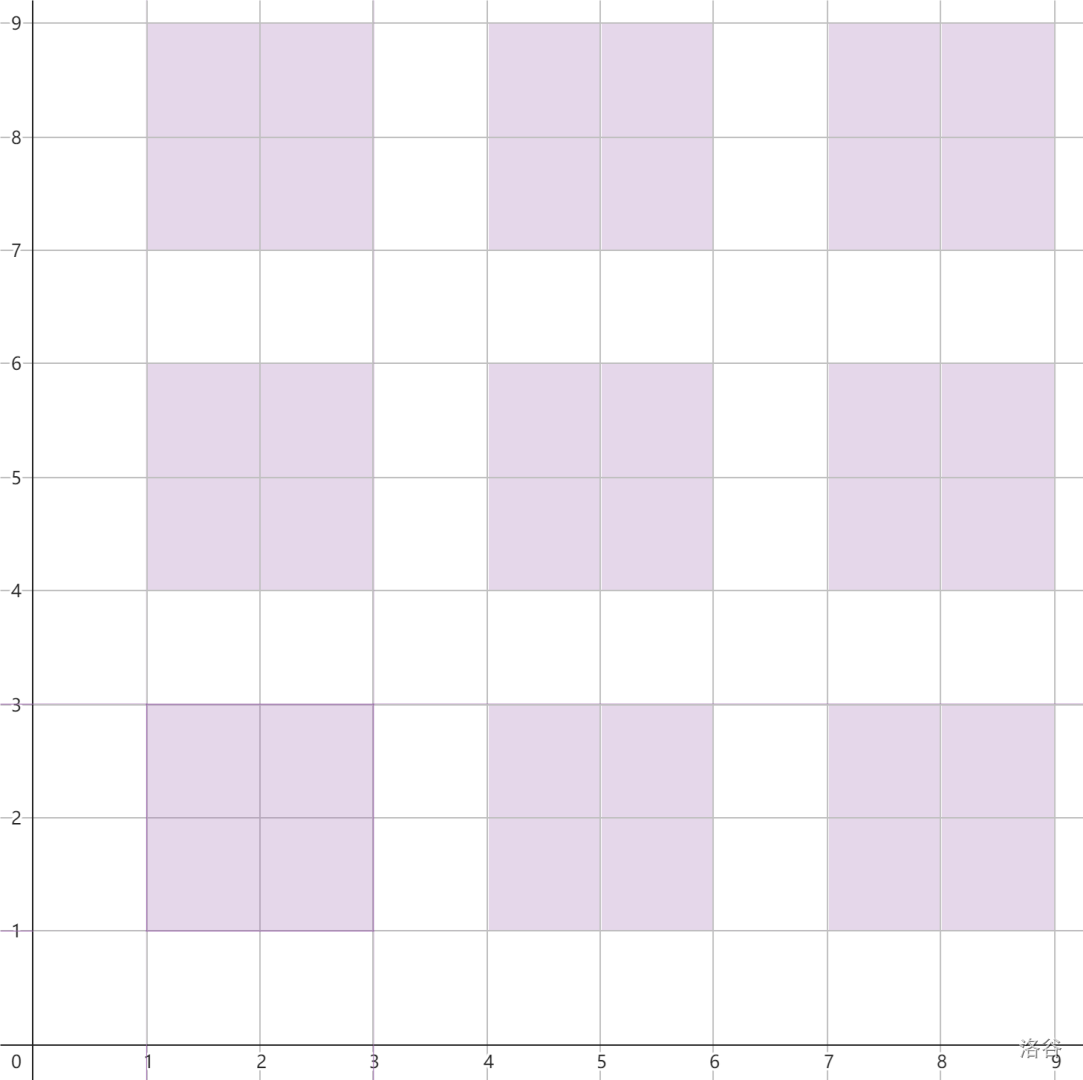
有一个位于第一象限的食堂。 食堂被划分为若干个 $1\times 1$ 的区域，区域 $(x,y)$ 为以 $(x,y),(x,y+1),(x+1,y),(x+1,y+1)$ 为顶点的正方形。称两个区域 $(x_1,y_1)$ 和 $(x_2,y_2)$ **相邻**当且仅当 $|x_1-x_2|+|y_1-y_2|=1$。 区域有两种类型，一种是可供顾客自由走动的过道，另一种是可供顾客坐下用餐的座位。食堂里的座位非常多，而且排布得很有规律：所有满足 $x\bmod 3\ne 0$ 且 $y\bmod 3\ne 0$ 的区域 $(x,y)$ 是座位，其他区域都是过道。四个相连的座位构成一张餐桌。 从上空俯瞰，食堂中座位的排布方式如下图：  在过道上，顾客可以自由移动。具体地，如果顾客当前位于过道 $(x,y)$，他可以走一步，移动到相邻的区域。如果顾客移动到了座位，他就会在此坐下。 顾客对座位的偏好可以用容忍度 $o\in\{0,1,2\}$ 来描述，其中： - $o=0$ 的顾客只愿意坐到对应**餐桌**没有人的**空座位**上吃饭。 - $o=1$ 的顾客只愿意坐到相邻**座位**没有人的**空座位**上吃饭。 - $o=2$ 的顾客愿意坐在任何**空座位**上吃饭。 当一个顾客坐下之后，他就会专注地吃饭，就算有其他顾客出现，导致当前的座位变成他不愿意坐的座位，他也不会因此离开。 最开始的时候，餐厅里一个顾客也没有。接下来**依次**发生了 $q$ 个事件，每个事件是以下两种之一： - 第一种事件：具有某个容忍度 $o$ 的顾客从区域 $(0,0)$ 进入餐厅，他会寻找移动步数最少的、他愿意坐的座位坐下，如果这样的座位有多个，顾客会选择 $x$ 坐标最小的，如果还有多个则会选择 $y$ 坐标最小的。 - 第二种事件：座位 $(x,y)$ 的状态发生了变化，如果原来有顾客坐在这里，这个顾客会立刻离开餐厅；如果原来这个座位上没有顾客，则会出现一个顾客坐在这里。 你需要对于第一种事件求出顾客选择的座位，对于第二种事件求出是有人离开还是有人坐下。

第一行一个正整数 $q\ (1\le q\le5\times10^5)$。 接下来 $q$ 行，每行先是一个整数 $t\in\{1,2\}$，表示事件种类。 当 $t=1$ 时，接下来读入一个整数 $o\in\{0,1,2\}$，表示来了一位容忍度为 $o$ 的顾客。 当 $t=2$ 时，接下来读入两个正整数 $x,y\ (1\le x,y\le10^4)$，满足 $x\bmod3\in\{1,2\}$ 与 $y\bmod3\in\{1,2\}$，表示座位 $(x,y)$ 的状态发生了变化。

对每个操作输出一行。 - 对于 $t=1$ 的操作，依次输出两个整数 $x,y$，表示顾客坐到了座位 $(x,y)$。 - 对于 $t=2$ 的操作，如果该座位上有人，输出 `out`，否则输出 `in`。

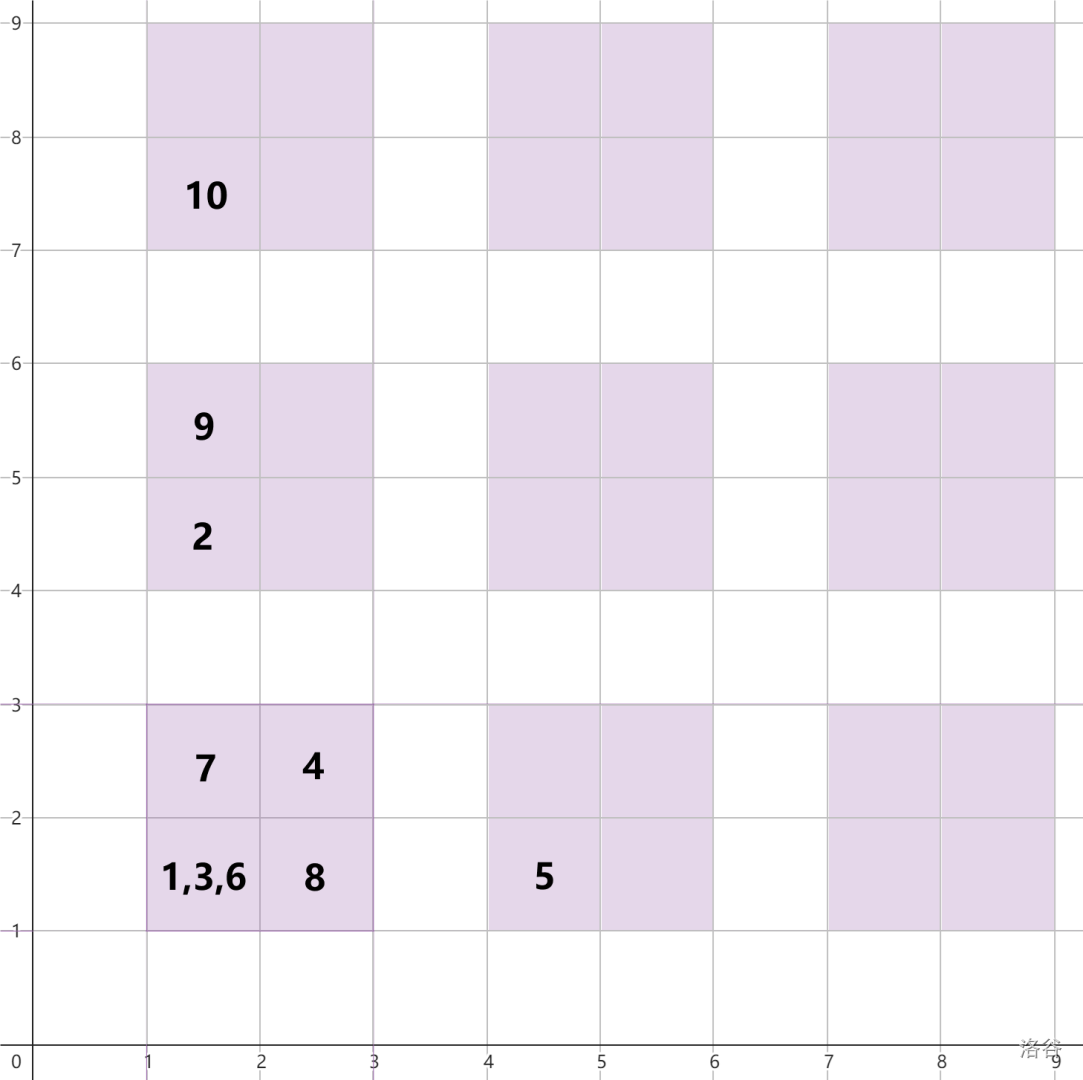
### 样例 #1 解释 以下图片展示了每一步操作影响的位置。数字标识了操作的编号。  ### 来源与致谢 来自 THUPC2025（2025 年清华大学学生程序设计竞赛暨高校邀请赛）决赛。感谢 THUSAA 的提供的题目。 数据、题面、标程、题解等请参阅 THUPC 官方仓库 。