P12077 [OOI 2025] Strong Connectivity Strikes Back

[试题来源](https://inf-open.ru/2024-25/final-materials/)。

有向图的顶点 $u$ 和 $v$ 被称为强连通的，如果存在一条从 $u$ 到 $v$ 的路径，并且存在一条从 $v$ 到 $u$ 的路径。注意，如果 $u$ 和 $v$ 强连通，且 $v$ 和 $w$ 强连通，那么 $u$ 和 $w$ 也强连通。因此，图中的顶点被划分为若干个强连通分量。属于同一个强连通分量的顶点彼此强连通（包括其本身），并且与任何不属于该分量的顶点都不强连通。 在一次图论课上，Alice 在黑板上画了一个包含 $n$ 个顶点的有向图，并且高亮了图中的强连通分量。课间，Bob 决定恶作剧，他想删除图中一些边的方向，并且希望 Alice 能够根据剩下的边和课间的强连通分量划分，唯一地恢复这些被删除方向的边。 帮助 Bob 确定最大可以删除的边数，以及可以删除这些边的方案数。 更正式地说，找到一个边的子集 $A$，使得如果我们删除集合 $A$ 中边的方向，则根据剩下的边的方向以及强连通分量的划分信息，可以唯一地恢复集合 $A$ 中边的方向，从而保持图的强连通分量不变。并且，求出这个子集 $A$ 的最大大小，以及这个子集的方案数。 由于这样的方案数可能非常大，输出该数对 $10^9 + 7$ 取模的结果。 如果正确计算了最大子集的大小，但方案数计算错误，则将获得部分分数。

第一行包含三个整数 $n$、$m$ 和 $g$（$2 \le n \le 2000$，$1 \le m \le 2000$，$0 \le g \le 7$）—— 图中的顶点数、边数以及测试组编号。 接下来 $m$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$，$u_i \neq v_i$）—— 第 $i$ 条边的起点和终点。 保证对于任意的 $1 \le i, j \le n$，$ (u_i, v_i) \neq (u_j, v_j)$ 且 $ (u_i, v_i) \neq (v_j, u_j)$，即任意两点之间最多有一条边，无论方向如何。

输出两行。 第一行输出一个整数——可以删除的最大边子集的大小。 第二行输出一个整数——该子集的方案数对 $10^9 + 7$ 取模的结果。如果你不想输出方案数，则在第二行输出任意一个从 $-1$ 到 $10^9 + 6$ 之间的数字。若第二行没有输出正确的数字，则无论子集大小是否正确，都会被判定为“错误答案”，并且该测试得分为零。

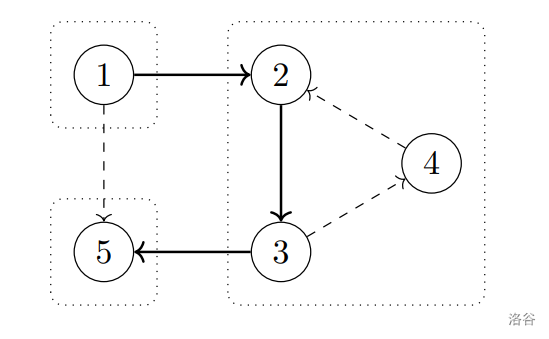
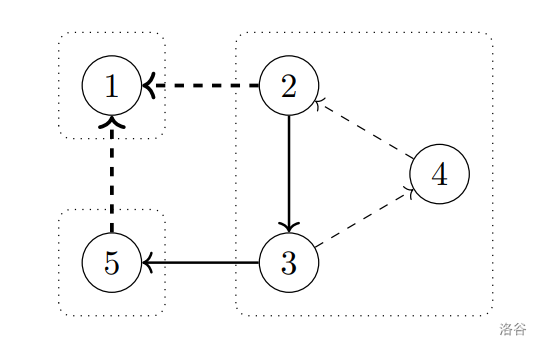
**样例解释** 在这个样例中，图的强连通分量如下图所示：  可以删除虚线边的方向。实际上，边 $(1, 5)$ 不能反向，因为如果反向，顶点 $1$、$2$、$3$、$5$ 将属于同一个强连通分量。同样，边 $(3, 4)$ 和 $(4, 2)$ 也不能反向，因为这样 $2$、$3$、$4$ 将不属于同一个强连通分量。 现在，考虑一个错误的子集选择方式：  这里，虚线加粗边的方向不能删除。例如，如果我们将边 $(1, 2)$ 和 $(1, 5)$ 的方向反向，得到的图依然会有相同的强连通分量划分。 可以证明，有 $4$ 条边的方向不能删除，因此正确答案是 $3$。 **评分** 本题的测试点共包含七个分组。分组的分数规则如下： 如果正确计算了最大边子集的大小和该子集的方案数，并且在该分组的所有测试点中都正确，用户将获得该分组的满分。 如果正确计算了最大子集的大小，但方案数计算错误，则将为该分组获得部分分数。此时，依赖该分组的分组也将进行测试，并且可能获得满分。 | 组别 | 部分分数 | 满分分数 | 限制条件：$n$ | 限制条件：$m$ | 依赖组别 | 说明 | | :--- | :------- | :------- | :----------- | :----------- | :------- | :---------------------------- | | 0 | 0 | 0 | -- | -- | -- | 样例测试点。 | | 1 | 7 | 11 | $n \le 14$ | $m \le 14$ | 0 | | | 2 | 5 | 9 | $n \le 20$ | $m \le 20$ | 0, 1 | | | 3 | 8 | 12 | -- | -- | -- | 满足 $u_i < v_i$，对于所有 $1 \le i \le n - 1$，存在一条边 $(i, i + 1)$。 | | 4 | 8 | 13 | -- | -- | 3 | 满足 $u_i < v_i$。 | | 5 | 12 | 20 | -- | -- | -- | 对于所有 $1 \leqslant i \leqslant n - 1$，存在一条边 $(i, i + 1)$，且存在一条边 $(n, 1)$。 | | 6 | 13 | 21 | -- | -- | 5 | 图是一个强连通分量。 | | 7 | 8 | 14 | -- | -- | 0 -- 6 | |