P12094 [NERC2024] Cactus without Bridges

一年前，Caroline 曾请求你帮她解决一个关于仙人掌图的问题。在过去的一年中，她对仙人掌图进行了深入研究。如今，轮到她来出题了。 给定一个**没有桥的仙人掌图**，并且**其中每一个奇环的长度都大于等于仙人掌图中奇环的数量**。你的任务是判断是否可以对仙人掌图的边进行正整数标号，使其满足以下条件： - 设最大标号为 $t$。所有整数 $1, 2, \ldots, t$ 都被用于标号（注意，不要求最小化或最大化 $t$ 的值）； - 对于仙人掌图中的每个顶点 $v$，与其相连的边所用的标号必须互不相同，且这些标号应构成一个连续整数区间。 图中的一条边称为**桥**，如果删去这条边会使图的连通分量数量增加。**仙人掌图**是一个连通的无向图，其中每条边至多只属于一个简单环。直观来说，仙人掌图是树的一种推广形式，允许存在一些环。仙人掌图中不允许出现重边（连接同一对顶点的多条边）或自环（连接自身的边）。

第一行包含两个整数 $n$ 和 $m$（$3 \le n \le 10^5$，$n \le m \le \left\lfloor \dfrac{3(n - 1)}{2} \right\rfloor$）——表示仙人掌图中的顶点数和边数。 接下来的 $m$ 行中，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \ne v$）——表示仙人掌图中的一条边。 所给的仙人掌图保证满足题目中的所有约束条件。

如果无法找到满足要求的标号方式，输出一行：`NO`。 否则，第一行输出 `YES`。第二行输出一个整数 $t$（$1 \le t \le m$）——表示使用的不同标号数量。第三行输出 $m$ 个整数 $c_i$（$1 \le i \le m$，$1 \le c_i \le t$）——表示每条边的标号顺序（与输入中的边顺序对应）。

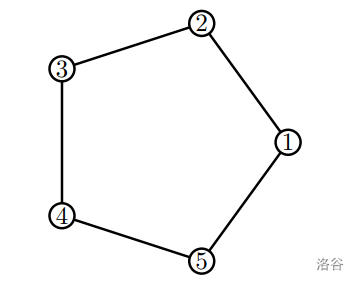
### 样例 1  ### 样例 2