P12100 [NERC2024] Incompetent Delivery Guy

在伊辛格，巫师萨鲁曼借助魔法设立了一套连接 $n$ 座高塔的传送系统。具体来说，他创建了 $m$ 条单向通道，每条通道连接两座高塔。第 $i$ 条通道需要 $t_i$ 秒，表示一只兽人通过这条通道所需的时间。换句话说，萨鲁曼的传送系统可以表示为一个带权有向图。 在 12 月 15 日，萨鲁曼正坐在中央高塔 $\textit{奥桑克}$（Orthanc）中，他通过魔法石（palantír）收到索伦的消息：一份贵重的礼物已经运抵伊辛格入口塔附近。于是，萨鲁曼需要指示守卫选出一只兽人，让他沿着从入口塔到奥桑克的最短路径将礼物送达。 不幸的是，兽人……并不是很聪明。虽然他们能够拖运货物穿越通道，理论上也知道奥桑克的位置，但他们对于“最短路径”的理解实在是相当贫乏。为了简化操作，萨鲁曼决定在某些塔上放置一个巨大的闪光指示牌，写着“$\textbf{前往奥桑克 —— 此路}$”，并指向通往某条通道的方向。 萨鲁曼希望兽人尽可能快地到达奥桑克，因此指示牌**只能指向某条通往奥桑克最短路径上的通道**。形式化地说，如果塔 $u$ 上的指示牌指向通道 $\vec{a} = \overrightarrow{uv}$，那么必须满足： $$ \mathop{\overrightarrow{\mathrm{dist}}}(v, O) < +\infty \quad \text{且} \quad \mathop{\overrightarrow{\mathrm{dist}}}(u, O) = t_{\vec{a}} + \mathop{\overrightarrow{\mathrm{dist}}}(v, O) $$ 其中，$\mathop{\overrightarrow{\mathrm{dist}}}(x, y)$ 表示从塔 $x$ 到塔 $y$ 的最短传送时间（若无法到达，则为 $+\infty$），$O$ 表示奥桑克所在的高塔编号，$u,v$ 分别为通道的起点和终点。 注意：萨鲁曼不会在奥桑克本身，也不会在从无法到达奥桑克的塔上设置指示牌。其余所有塔上，萨鲁曼将恰好设置一个指向某条合规通道的闪光指示牌。 即便如此，事情也并不总是顺利。每当一只兽人准备前往奥桑克时，他在经过每一座塔（除奥桑克外）时，要么选择跟随萨鲁曼设置的闪光指示牌前进，要么进行一次所谓的“$\textit{随意乱走}$”行为，即随机选择一条通道离开当前塔。 对于任意一只兽人，存在一个整数 $d$，表示他在整个传送过程中最多会进行 $d$ 次“随意乱走”。我们将这个值称为这只兽人的“$\textit{无能度}$”。 如果某一时刻兽人到达一座无法通往奥桑克的塔，那么他会发现该塔没有任何指示牌。此时，即便是最“有能”的兽人也会意识到任务失败，立即停止前进并等待救援。 萨鲁曼深知他的仆人们都不太聪明，所以他并不指望送货能很快完成，但他希望至少能**保证送达**。因此，有必要选择一只无能度尽可能大的兽人完成任务。但另一方面，真正聪明的兽人极为稀少，把他们从其他岗位调走会严重影响其他安排。 于是，给定伊辛格的传送系统，请你帮萨鲁曼找出一个最优策略安排指示牌，使得从入口塔（编号为 $1$）出发的兽人在**无能度为 $d$ 的前提下，必然可以成功到达奥桑克（编号为 $n$）**。请你求出这个最大可能的 $d$ 值。

第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 4 \cdot 10^5$，$0 \le m \le 4 \cdot 10^5$），分别表示塔的数量和通道的数量。 接下来 $m$ 行，每行包含三个整数 $u_i$、$v_i$ 和 $t_i$（$1 \le u_i, v_i \le n$，$1 \le t_i \le 10^6$），表示从塔 $u_i$ 到塔 $v_i$ 有一条传送时间为 $t_i$ 秒的单向通道。 可能存在多条通道连接相同的两个塔（同向或反向），也可能存在指向自身的通道（自环）。 塔 $1$ 为入口塔，塔 $n$ 为奥桑克。

输出一个整数 $d$，表示满足题意的最大无能度。 如果任意无能度下都可以成功送达，输出 $n$；如果任意无能度下都无法送达，输出 $-1$。

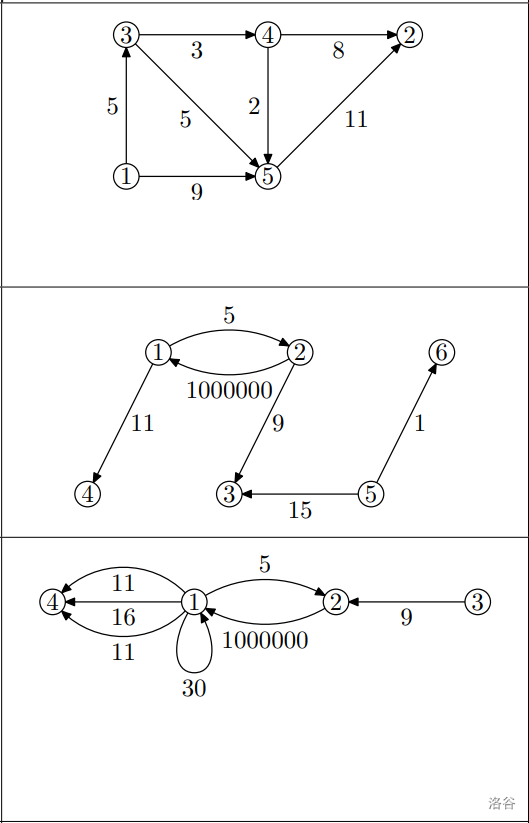
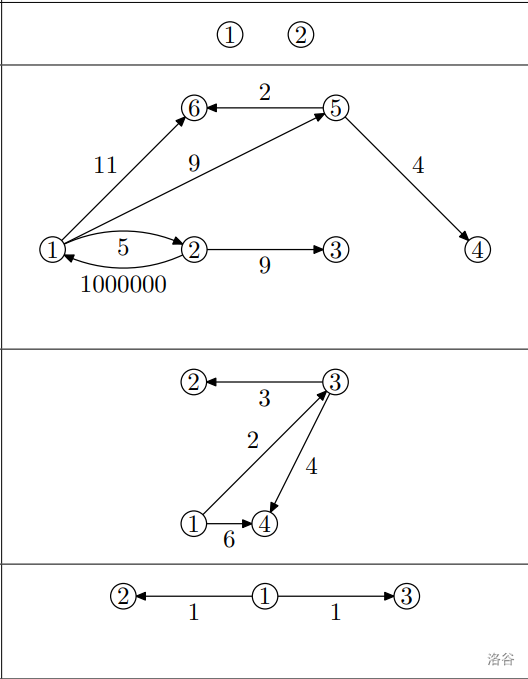
样例图示如下：