P12104 [NERC2024] Managing Cluster

You want to write a cluster manager extension that will improve your product performance. Your product has $n$ services (numbered from $1$ to $n$) and is hosted on a cluster with $2n$ machines (numbered from $1$ to $2n$). Each service is running in exactly two replicas. Each replica is run on some machine. Each machine runs exactly one replica of some service. One of the key factors of this cluster's performance is the network. Some pairs of machines are connected directly and can transfer data between them very efficiently. There are exactly $2n-1$ direct connections, and it is possible to transfer data between any two machines using direct connections. In other words, direct connections form a tree. During the deployment, all $2n$ replicas were assigned to machines. Your extension gets the direct connections list and the sequence $a_1, a_2, \ldots, a_{2n}$, where $a_i$ is the number of the service that will be running on machine $i$. Your extension can swap some replicas between machines. The swap operation takes two machines $i$, $j$ and swaps values $a_i$ and $a_j$. Each machine is allowed to participate in at most one swap operation. Your extension should make some swap operations that maximize the cluster performance. Due to the fact that most data will be transferred between two replicas of the same service, the cluster performance is measured as the number of services that have two replicas running on machines connected directly. Help to write the extension that will maximize the cluster performance.

The first line contains a single integer $T$ ($1 \leq T \leq 10^5$) --- the number of test cases. Descriptions of test cases follow. The first line of each test case contains a single integer $n$ ($1 \leq n \leq 10^5$). The second line contains $2n$ integers $a_1, a_2, \ldots, a_{2n}$ ($1 \leq a_i \leq n$). It is guaranteed that each value from $1$ to $n$ appears exactly twice in this sequence. Each of the next $2n-1$ lines contains two integers $u$ and $v$ ($1 \leq u, v \leq 2n$, $u \neq v$), meaning that machines $u$ and $v$ are connected directly. Direct connections are guaranteed to form a tree. It is guaranteed that the sum of $n$ for all test cases does not exceed $10^5$.

For each test case on the first line print a single integer $k$ ($0 \leq k \leq n$) --- the number of swap operations the extension wants to make. Each of the next $k$ lines should contain two integers $i$, $j$ ($1 \leq i, j \leq 2n$, $i \neq j$) --- swap operations. Each number from $1$ to $2n$ should appear at most once. Note that the order of operations is not important. After applying swap operations, the cluster performance should be the maximum possible. You can print any answer that satisfies the requirements.

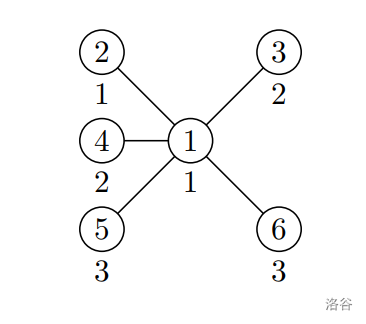
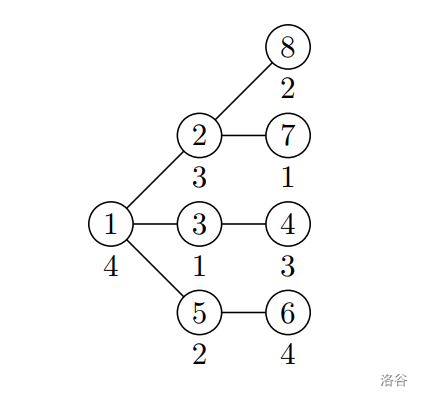
In the first test case only replicas of service 2 run on directly connected machines, so the performance is 1. The performance can be increased to 2 by swapping replicas between machines 1 and 3.  In the second test case no two replicas run on directly connected machines, so the performance is zero. The performance can be increased to 3 by performing swaps $1-5$, $8-3$, and $4-7$ so that replicas of services 2, 3, and 4 run on directly connected machines. It can be shown that it is impossible to get performance 4 here.  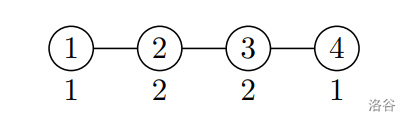In the third test case only replicas of service 1 run on directly connected machines, so the performance is 1. It is obvious that here the performance cannot be made any bigger.