P12109 [NWRRC2024] Eight-Shaped Figures

*看到过去两年"K 字形图形"和"H 字形图形"的问题后，你认真对待了这个警告。你做好了充分准备。对于字母表中剩下的 24 个字母，你都设想了可能出现的题目。你甚至实现了所有 24 个解决方案，并耗尽了数字团队参考文档的所有空间，就为了把这些代码带到比赛现场。如果评委们如此缺乏创意，又出了一道关于字母形状的题目，你就能在第 1 分钟提交通过，让所有人都困惑不已。* *什么，又是图形题？真的吗？！哈哈！哦...等等...*

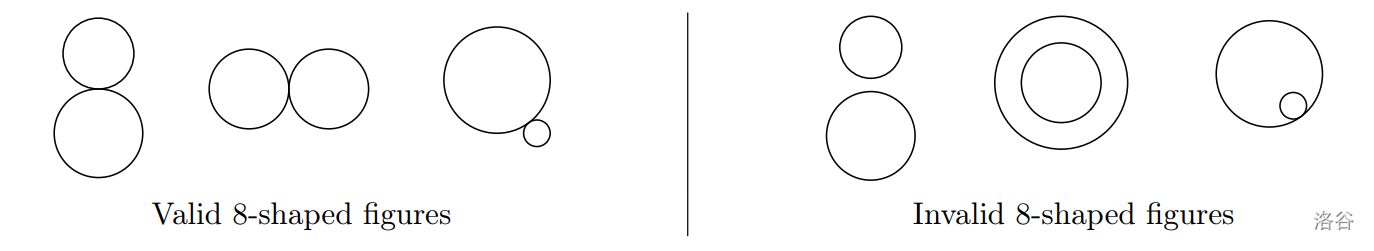
我们定义平面上的两个圆构成一个 $\textit{8 字形图形}$，当且仅当它们彼此相切，且没有一个圆完全位于另一个圆内部。  给定平面上 $n$ 个圆的集合。任意两个圆最多有一个公共点。换句话说，任意两个圆不会相交两次或重合，但它们可以相切或一个圆位于另一个圆内部。 请计算这些圆中有多少对构成了 8 字形图形。

每个测试包含多个测试用例。第一行包含测试用例数量 $t$（$1 \le t \le 10^4$）。接下来是各测试用例的描述。 每个测试用例的第一行包含一个整数 $n$，表示圆的个数（$2 \le n \le 2 \cdot 10^5$）。 接下来的 $n$ 行中，第 $i$ 行包含三个整数 $x_i$、$y_i$ 和 $r_i$，分别表示第 $i$ 个圆的圆心坐标和半径（$-10^9 \le x_i, y_i \le 10^9$；$1 \le r_i \le 10^9$）。任意两个圆不会相交两次或重合，但它们可以相切或一个圆位于另一个圆内部。 保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出构成 8 字形图形的圆的对数。