P12111 [NWRRC2024] Game of Annihilation

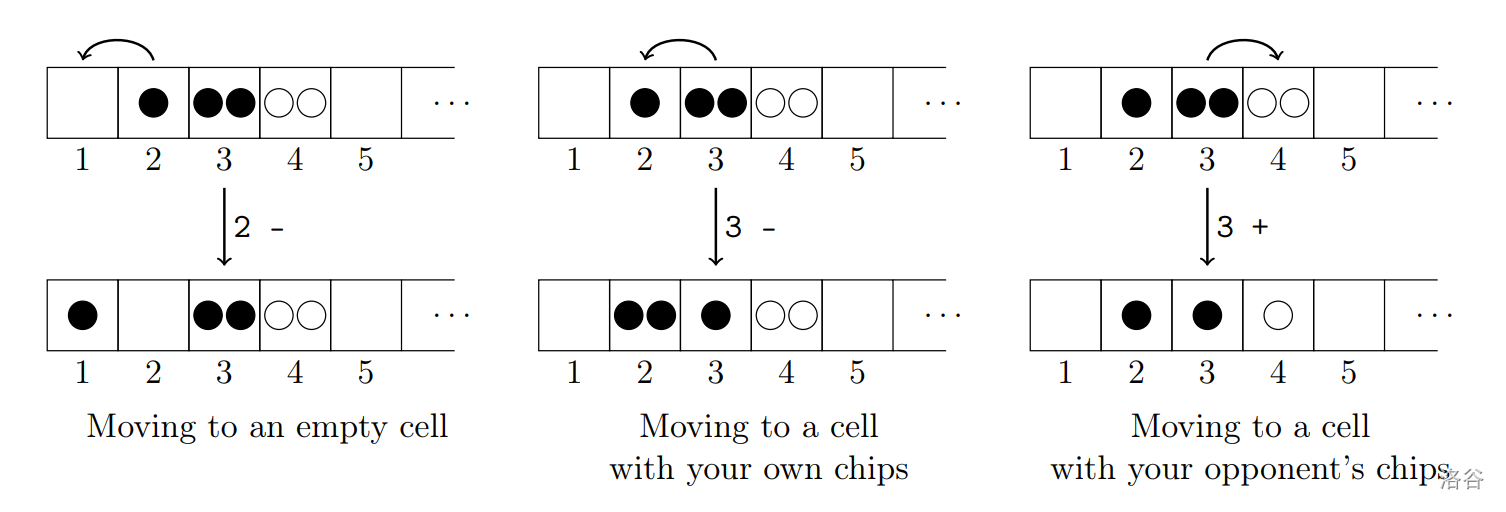
两名玩家在一个向右无限延伸的纸带上进行游戏。纸带被划分为编号为 $1, 2, 3, \ldots$ 的格子，从左到右排列。每个格子 $x$ 与 $x - 1$ 和 $x + 1$ 相邻，除了格子 $1$ 只与格子 $2$ 相邻。 纸带上放置有有限数量的红色筹码（先手玩家的筹码）和蓝色筹码（后手玩家的筹码）。每个格子要么包含多个红色筹码，要么包含多个蓝色筹码，要么为空。 玩家轮流行动。在自己的回合中，玩家可以选择跳过回合，或者移动自己的一个筹码到相邻格子。如果目标格子没有对手的筹码，回合结束；如果目标格子有至少一个对手筹码，则双方各移除一个筹码——因此回合结束时，同一格子中仍不会存在不同颜色的筹码。  如果双方筹码都耗尽，游戏以平局结束。如果仅一方筹码耗尽，则该方判负，对手获胜。若经过 $10^{100}$ 回合后游戏仍未结束，则强制判定为平局。 给定纸带的初始状态，确定在双方都采取最优策略的情况下谁会获胜，并找出先手玩家的任意最优首步行动。

每个测试包含多个测试用例。第一行给出测试用例数量 $t$（$1 \le t \le 10^4$）。随后是各测试用例的描述。 每个测试用例的第一行包含一个整数 $n$，表示初始有筹码的格子数量（$2 \le n \le 2 \cdot 10^5$）。 接下来的 $n$ 行中，第 $i$ 行包含两个整数 $x_i$, $m_i$ 和一个字符 $c_i$，分别表示从左数第 $i$ 个非空格子的坐标、筹码数量和颜色（$1 \le x_1 < x_2 < \cdots < x_n \le 10^6$；$1 \le m_i \le 10^6$；$c_i \in \{\mathtt{R}, \mathtt{B}\}$）。纸带上至少有一个红色和一个蓝色筹码。 保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出： - $\texttt{First}$ $x$ $d$，如果先手玩家（红色筹码）将获胜； - $\texttt{Second}$，如果后手玩家（蓝色筹码）将获胜； - $\texttt{Draw}$ $x$ $d$，如果游戏将以平局结束。 在第一种和第三种情况下，$x$ $d$ 分别表示任意致胜或致和的首步行动——即在采取该行动后，面对后手玩家的最优策略，仍有可能获胜或达成平局。其中 $x$ 表示应移动的红色筹码坐标，$d \in \{\texttt{-}, \texttt{+}\}$ 表示移动方向（$\texttt{-}$ 表示移动到 $x - 1$，$\texttt{+}$ 表示移动到 $x + 1$）。若 $d$ 为 $\texttt{-}$，则 $x$ 必须大于 $1$。若建议先手玩家跳过回合，则输出 $\texttt{0 0}$ 代替 $x$ $d$。 输出字母大小写不限：例如 $\texttt{First}$、$\texttt{FIRST}$、$\texttt{fiRST}$ 都会被判题器视为等效。

在最后一个测试用例中，除了 $\texttt{1 +}$ 外只有 $\texttt{0 0}$（跳过回合）一种可能行动。虽然这是致和行动，但不会被接受为有效输出。