P12120 [NordicOI 2025] 时之预言 / Xoracle

目前本题交互库有误。

**这是一道交互题。** 很久以前，在北欧诸国的中心地带，有一位名叫罗尼的勇敢战士。罗尼以其无畏的勇气和敏锐的头脑闻名，常常能解开连最睿智的贤者都束手无策的谜题。有一天，罗尼被召集到一片古老的森林，那里屹立着一棵神秘的树。这棵树非同寻常——它完全隐形，其节点和分支对凡人之眼不可见。树的每个节点上都居住着一位古老的精灵，而每个节点的度数（degree）是理解树结构的关键。 王国的预言者，被称为**神秘树预言者**（Xoracle），是一个强大的存在，但它只能回答一种类型的问题： 「告诉我节点 A 和节点 B 的度数的按位异或结果。」 凭借这些神秘的信息，罗尼必须推导出树中所有 $N$ 个节点的度数，以征服古老的精灵并揭开树的秘密。然而，神秘树预言者最多只会回答 $Q$ 次询问，之后便会永远封存其智慧。 罗尼的任务是利用神秘树预言者的回答，确定这棵隐形树中所有节点的度数。这棵树有 $N$ 个节点和 $N-1$ 条边，是连通的，也就是说，任意一对节点之间都存在路径。节点的度数是指与该节点相连的边的数量。通过策略性地选择节点对并解读它们度数的按位异或结果，罗尼希望能重构树中所有节点的度数。 ## 交互方式 你的程序首先需要读取一行输入，包含两个空格分隔的整数 $N$ 和 $Q$，分别表示树中的节点数量和你最多可以向神秘树预言者提出的询问次数。树的节点编号从 $1$ 到 $N$。 接下来，你的程序可以进行最多 $Q$ 次询问。要提出一个询问，你的程序需要输出一行，格式为 `? i j`，其中 $1 \leq i, j \leq N$。评测程序随后会返回一行，包含一个数字 $x$，其中 $x=\operatorname{deg}(i) \oplus \operatorname{deg}(j)$。这里 $\operatorname{deg}(x)$ 表示节点 $x$ 的度数，$\oplus$ 表示按位异或运算。 两个整数 $a$ 和 $b$ 的按位异或结果是通过查看它们的二进制表示计算出来的。第 $i$ 位的结果为 $1$，当且仅当 $a$ 或 $b$ 的第 $i$ 位有且仅有一个为 $1$。在 C++ 和 Python 中，这一运算符均为 ^。 在完成询问后，你的程序必须输出所有节点的度数。输出的方式是：另起一行，输出 !，后跟一个空格和 $N$ 个空格分隔的整数，表示所有 $N$ 个节点的度数（顺序不限）。 输出度数的操作不会计入你的程序允许的询问次数。 为了接收询问的答案并在最后提交度数，你的程序需要刷新输出缓冲区。可以通过以下方式实现： - C++：`std::cout

无

无

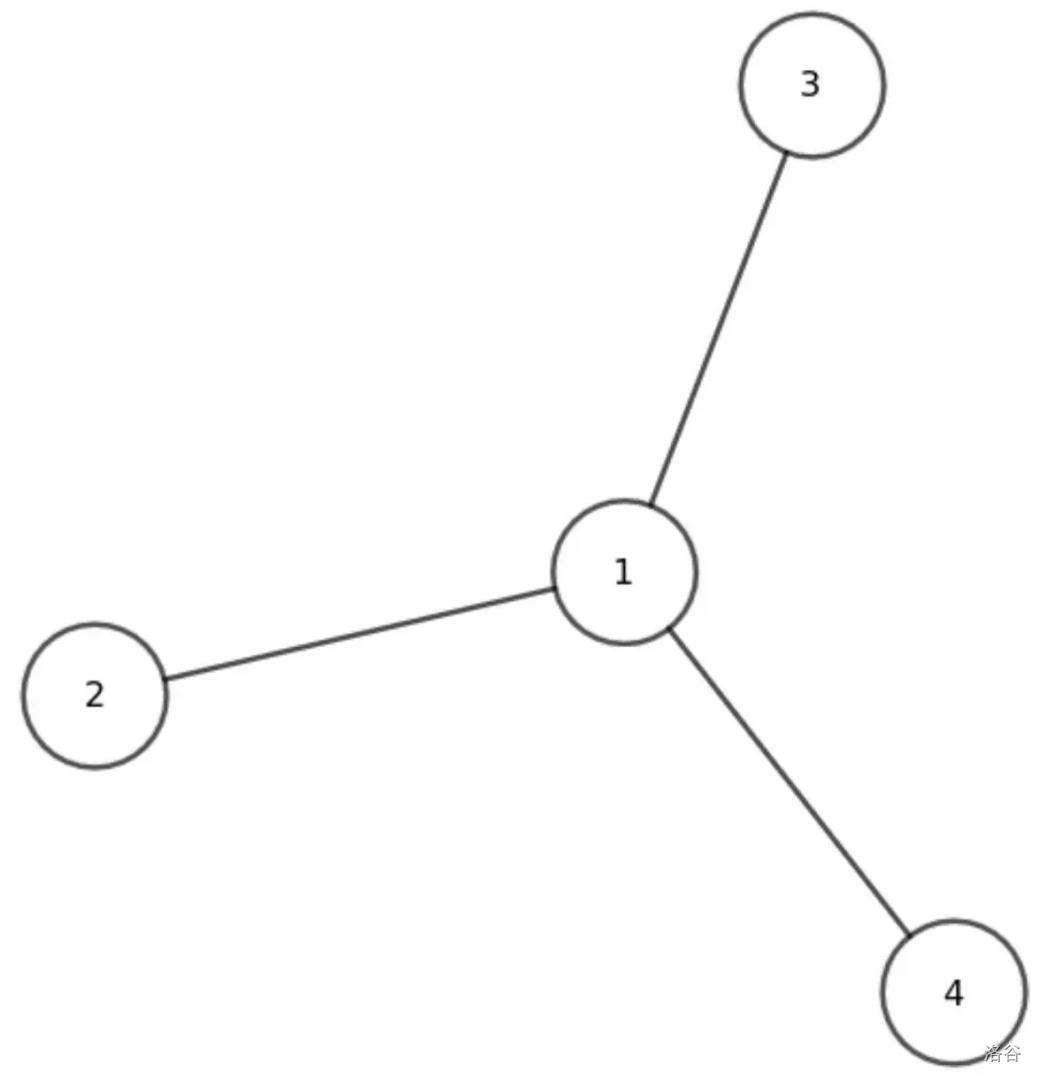
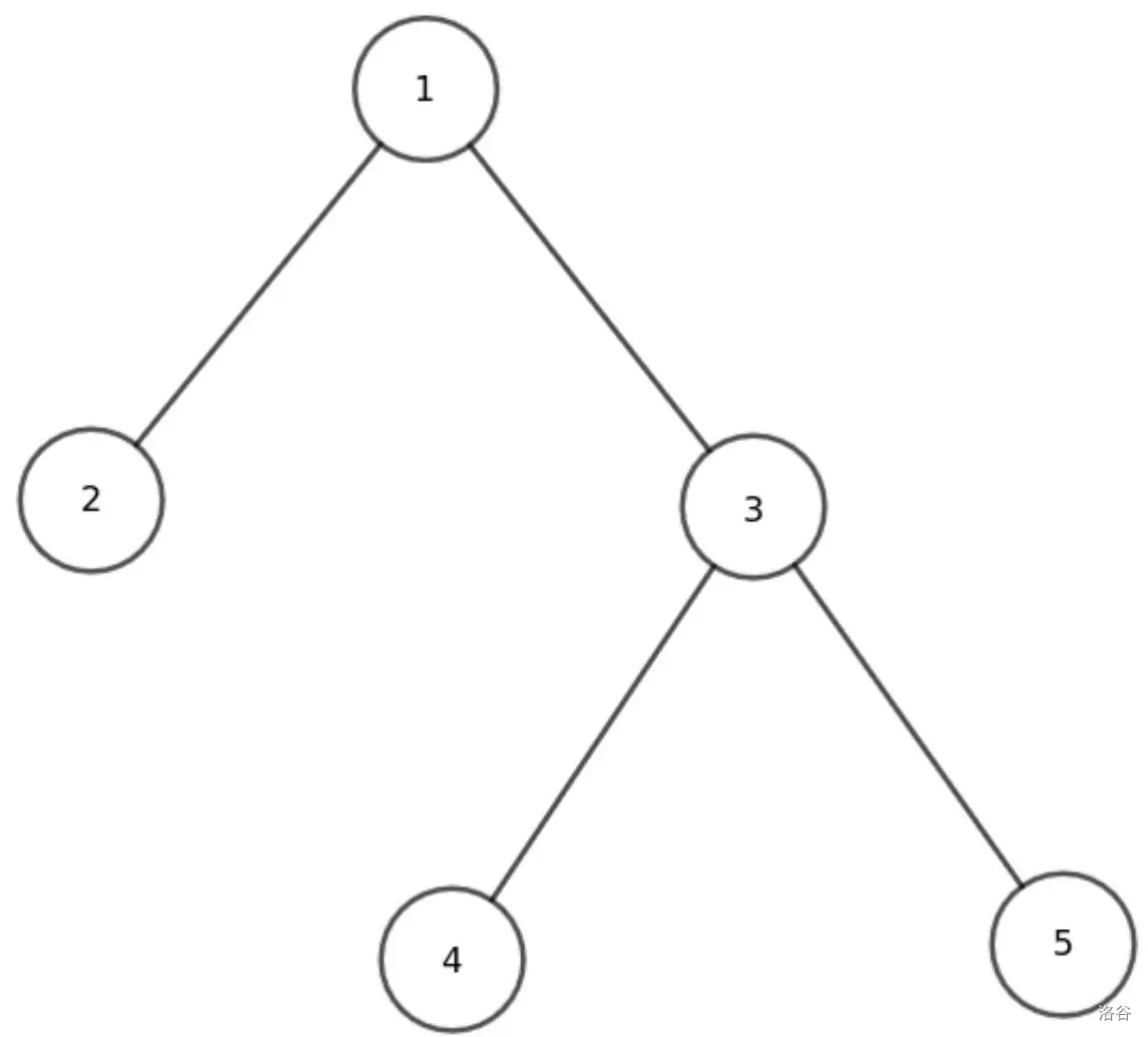
【样例解释】 #### 样例 $1$ 请观察图 1 中所示的树。 以下是你与评测程序的交互过程，其中 > 表示评测程序的输出，< 表示你的程序的输出。 - 首先，输入提供 $N$ 和 $Q$ 的值。 - 接着，你对节点 $2$ 和 $4$ 提出询问，得到结果 $0$。 - 然后，你对节点 $4$ 和 $1$ 提出询问，得到结果 $2$。 - 接着，你对节点 $3$ 和 $3$ 提出询问，得到结果 $0$。 - 最后，你的程序输出树的度数为 $1,3,1,1$，这是正确的。（注意，度数的输出顺序可以是任意的。）  #### 样例 $2$： 请观察图 2 中所示的树。 以下是你与评测程序的交互过程，其中 > 表示评测程序的输出，< 表示你的程序的输出。  **注意**：样例中给出的询问不一定能保证推导出正确的答案。 【数据范围与约定】 对于所有数据，满足： - $2 \leq N \leq 10^{5}$。 详细子任务附加限制及分值如下表所示： | 子任务编号 | 分值 | 附加限制 | | :-----------: | :-----------: | :-----------: | | $1$ | $8$ | 任意节点的度数最大为 $3$，且树中至少存在度数为 $1$、$2$ 和 $3$ 的节点。$N\le 1000,Q=N-1$ | | $2$ | $5$| 任意节点的度数最大为 $4$，且树中至少出现 $4$ 种可能度数中的 $3$ 种。$N\le 1000,Q=N-1$ | | $3$ | $9$|$Q=N^2,N\le 300$ | |$4$ | $11$|$Q=35000,N\le 1000$ | | $5$ | $24$|$Q=N-1,N\le 1000$ | |$6$ | $43$ |$Q=N-1$ |