P1212 [USACO1.4] Packing Rectangles

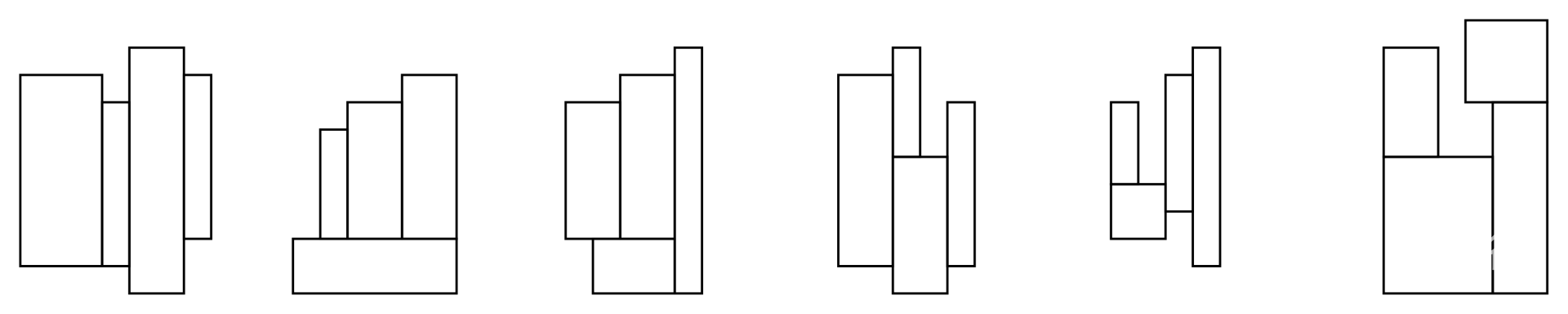
Given $4$ rectangles, find a smallest enclosing rectangle that can contain all $4$ rectangles without overlap. By “smallest” we mean the area is minimal.  For any of the $4$ rectangles, its sides must be parallel to the sides of the enclosing rectangle. The figure above shows $6$ ways to pack the $4$ rectangles. These $6$ layouts are the only possible basic layouts. Any other layout can be obtained from a basic one by rotation or mirror reflection. There may be multiple enclosing rectangles that satisfy the conditions and have the same area; you should output the side lengths of all such enclosing rectangles.

There are $4$ lines, each containing two positive integers, representing the side lengths of each rectangle.

The total number of lines equals the number of solutions plus one. The first line is an integer, representing the minimal area of the enclosing rectangle. Each of the following lines describes one solution, represented by $p,q\space (p \leqslant q)$. These lines must be sorted in ascending order by $p$, and all lines must be distinct.

Constraints For $100\%$ of the testdata, all input numbers are in [1, 50]. Problem translation from NOCOW. USACO Training Section 1.4. Translated by ChatGPT 5