P12153 【MX-X11-T7】「蓬莱人形 Round 1」信念

原题链接：。 --- >「此情可待成追忆 只是当时已惘然」

给定一棵大小为 $n$ 的有根树，点的编号 $1$ 到 $n$，根节点为 $1$ 号节点。 点 $i$ 有一个二元组 $(dep_i,str_i)$，其中 $dep_i$ 表示 $i$ 到根的距离，$str_i$ 表示从根节点到 $i$ 的简单路径上的所有节点的编号顺次连接组成的一个**字符集为点的编号**的字符串。 有 $q$ 次询问，每次询问给定 $x$ 和 $k$，请你输出 $f(x,k)$ 的值，$f(x,k)$ 的计算方式如下： 1. 求出 $(x,k)$ 邻域内的点的编号集合 $S$。 2. 将 $S$ 中的点按照其二元组升序排序（即以 $dep$ 为第一关键字，以 $str$ 的字典序为第二关键字从小到大排序），排序后的点记为 $c_1,c_2,\ldots,c_{|S|}$。 3. $f(x,k)$ 的值即为 $\sum_{i=1}^{|S|-1} \operatorname{Dis}(c_i,c_{i+1})$。 定义 $u$ 到 $v$ 的距离，即 $\operatorname{Dis}(u,v)$，为从 $u$ 到 $v$ 的树上唯一简单路径上的边数。 定义 $(u,d)$ 邻域表示树上与 $u$ 的距离 $\le d$ 的点集。

无

无

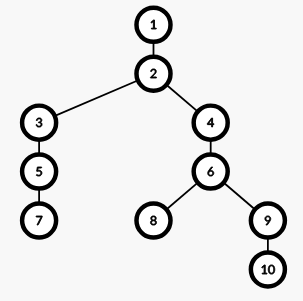
**【样例解释 #1】**  每个点的二元组如下所示（其中 $\mid$ 仅作为字符串中字符的区分方式）： | 节点编号 | 二元组 | | -------- | ------------------ | | $1$ | $(0,1)$ | | $2$ | $(1,1 \mid 2)$ | | $3$ | $(2,1 \mid 2 \mid 3)$ | | $4$ | $(2,1\mid 2\mid 4)$ | | $5$ | $(3,1\mid 2\mid 3\mid 5)$ | | $6$ | $(3,1 \mid 2 \mid 4 \mid 6)$ | | $7$ | $(4,1\mid 2\mid 3\mid 5\mid 7)$ | | $8$ | $(4,1\mid 2\mid 4\mid 6\mid 8)$ | | $9$ | $(4,1\mid 2\mid 4\mid 6\mid 9)$ | | $10$ | $(5,1\mid 2\mid 4\mid 6\mid 9\mid 10)$ | 对于第一组询问 $(1,3)$，其 $c$ 序列为 $1,2,3,4,5,6$，故 $f(1,3)=\operatorname{Dis}(1,2)+\operatorname{Dis}(2,3)+\operatorname{Dis}(3,4)+\operatorname{Dis}(4,5)+\operatorname{Dis}(5,6)=11$。 对于第二组询问 $(3,2)$，其 $c$ 序列为 $1,2,3,4,5,7$，故 $f(3,2)=8$。 对于第三组询问 $(4,3)$，其 $c$ 序列为 $1,2,3,4,5,6,8,9,10$，故 $f(4,3)=15$。 **【数据范围】** **本题使用子任务捆绑**。 对于所有的测试数据，满足 $1\le n,q\le 5\times 10^5$，$1\le p_i