P12153 【MX-X11-T7】Faith

原题链接：。 --- >「此情可待成追忆 只是当时已惘然」

Given a rooted tree with $n$ nodes (numbered $1$ to $n$, root is node $1$). Each node $i$ has a pair $(dep_i, str_i)$ where: - $dep_i$ is the distance from $i$ to the root. - $str_i$ is the string formed by concatenating the IDs of all nodes along the simple path from the root to $i$ (**the character set consists of node IDs**). There are $q$ queries. For each query $(x, k)$, compute $f(x, k)$ as follows: 1. Find the set $S$ of node IDs in the $(x, k)$-neighborhood. 2. Sort $S$ in ascending order by their pairs (using $dep$ as the primary key and $str$'s lexicographical order as the secondary key). Let the sorted list be $c_1, c_2, \ldots, c_{|S|}$. 3. $f(x, k)$ is defined as $\sum_{i=1}^{|S|-1} \operatorname{Dis}(c_i, c_{i+1})$. **Definitions**: - $\operatorname{Dis}(u, v)$: The number of edges on the unique simple path between $u$ and $v$. - $(u, d)$-neighborhood: The set of nodes whose distance from $u$ is $\le d$.

- First line: Two integers $n, q$ (number of nodes and queries). - Second line: $n-1$ integers where the $i$-th integer is the parent $p_{i+1}$ of node $i+1$. - Next $q$ lines: Two integers $x, k$ per line (query parameters).

Output $q$ lines, each containing the answer to the corresponding query.

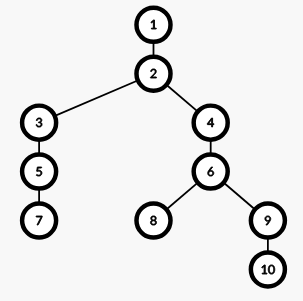
## Explanation #1  The pairs for each node are (where "|" is used only to separate characters in strings): | Node ID | Pair | |---------|-----------------------| | $1$ | $(0,1)$ | | $2$ | $(1,1 \mid 2)$ | | $3$ | $(2,1 \mid 2 \mid 3)$ | | $4$ | $(2,1\mid 2\mid 4)$ | | $5$ | $(3,1\mid 2\mid 3\mid 5)$ | | $6$ | $(3,1 \mid 2 \mid 4 \mid 6)$ | | $7$ | $(4,1\mid 2\mid 3\mid 5\mid 7)$ | | $8$ | $(4,1\mid 2\mid 4\mid 6\mid 8)$ | | $9$ | $(4,1\mid 2\mid 4\mid 6\mid 9)$ | | $10$ | $(5,1\mid 2\mid 4\mid 6\mid 9\mid 10)$ | For query $(1, 3)$: - $c$ sequence: $1,2,3,4,5,6$ - $f(1,3) = \operatorname{Dis}(1,2)+\operatorname{Dis}(2,3)+\operatorname{Dis}(3,4)+\operatorname{Dis}(4,5)+\operatorname{Dis}(5,6) = 11$. For query $(3, 2)$: - $c$ sequence: $1,2,3,4,5,7$ - $f(3,2) = 8$. For query $(4, 3)$: - $c$ sequence: $1,2,3,4,5,6,8,9,10$ - $f(4,3) = 15$. ## Constraints **This problem uses subtask scoring.** For all test data: $1 \le n, q \le 5 \times 10^5$, $1 \le p_i < i$, $1 \le x \le n$, $0 \le k \le n$. | Subtask | $n, q \leq$ | Special Property | Points | |---------|-------------|-------------------|--------| | 1 | $1000$ | None | 5 | | 2 | $2 \times 10^5$ | A | 25 | | 3 | $1 \times 10^5$ | B | 10 | | 4 | $1 \times 10^5$ | None | 15 | | 5 | $2 \times 10^5$ | None | 15 | | 6 | $5 \times 10^5$ | None | 30 | - **Special Property A**: Parent nodes are randomly generated within valid ranges. - **Special Property B**: All leaf nodes have the same depth. **Note:** Use fast I/O methods for this problem. Translated by DeepSeek R1