P12193 [NOISG 2025 Prelim] Ducks And Buttons

**Warning for C++ users: The large size of integers involved in this problem may require the use of the `long long` data type instead of the `int` data type.** Shor the Duck is playing a game with his friends! The game is played on a 1-dimensional grid consisting of $n$ cells in, arranged in a row and numbered from $1$ to $n$ from left to right. Each cell has a button. The button on cell $i$ will be permanently pressed if at any point in time there are at least $a[i]$ ducks on that cell. Even if the ducks leave, the button remains pressed. To win the game, all $n$ buttons must be pressed. Initially, there are $d$ ducks on cell $1$. In one move, a single duck can move one cell left or right. Determine the minimum total number of moves required to win the game. **It is guaranteed that it is possible to win the game with some number of moves.**

Your program must read from standard input. The first line of input contains two space-separated integers $n$ and $d$. The second line of input contains $n$ space-separated integers $a[1], a[2], \ldots, a[n]$.

Your program must print to standard output. Output a single integer, the minimum total number of moves required to win the game.

### Subtasks For all test cases, the input will satisfy the following bounds: - $1 \leq n \leq 200\,000$ - $1 \leq d \leq 10^9$ - $0 \leq a[i] \leq d$ for all $1 \leq i \leq n$ - It is possible to win the game with some number of moves. Your program will be tested on input instances that satisfy the following restrictions: | Subtask | Marks | Additional Constraints | | :-: | :-: | :-: | | $0$ | $0$ | Sample test cases | | $1$ | $8$ | $n = 2$ | | $2$ | $5$ | $a[i] = 0$ | | $3$ | $11$ | $a[i] \leq 1$ | | $4$ | $6$ | All values of $a[i]$ are equal | | $5$ | $19$ | $n, d \leq 1000$ | | $6$ | $12$ | $a[i]$ is non-decreasing | | $7$ | $16$ | $a[i]$ is non-increasing | | $8$ | $23$ | No additional constraints | ### Sample Test Case 1 Explanation This test case is valid for subtasks $1, 5, 7$, and $8$. ### Sample Test Case 2 Explanation This test case is valid for subtasks $3, 5$, and $8$. ### Sample Test Case 3 Explanation This test case is valid for subtasks $4, 5, 6, 7$, and $8$. ### Sample Test Case 4 Explanation This test case is valid for subtasks $5, 6$, and $8$. ### Sample Test Case 5 Explanation This test case is valid for subtasks $5, 7$, and $8$. ### Sample Test Case 6 Explanation This test case is valid for subtasks $5$ and $8$.  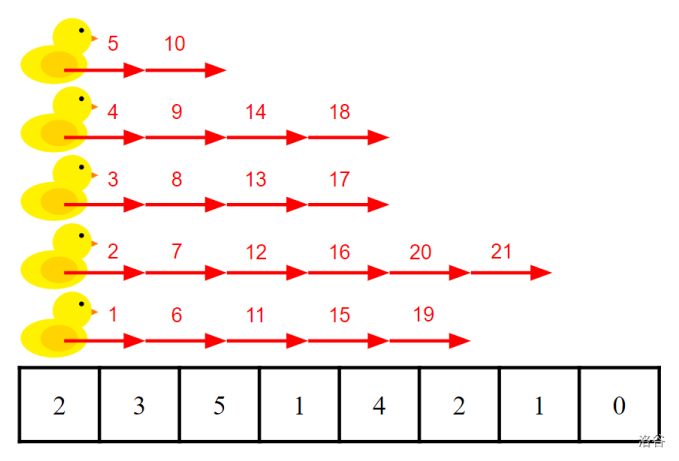One possible sequence of moves that minimises the total number of moves is shown above. Each red arrow is a move, and the number above it indicates the order of the moves, with move $1$ coming first. - Button $1$ is first pressed before any moves occur. - Button $2$ is first pressed after move $3$. - Button $3$ is first pressed after move $10$. - Button $4$ is first pressed after move $11$. - Button $5$ is first pressed after move $18$. - Button $6$ is first pressed after move $20$. - Button $7$ is first pressed after move $21$. - Button $8$ is first pressed before any moves occur (since $a[8] = 0$). Since all buttons are pressed by the end of all $21$ moves, $21$ moves is sufficient to win the game. It can be proven that $21$ moves is the minimum total number of moves needed. ### Sample Test Case 7 Explanation This test case is valid for subtasks $4, 6$, and $8$.