P12196 [NOISG 2025 Prelim] Lasers 2

Pavement has purchased a laser toy from Gohcart (who originally bought it from Rar the Cat). The toy features a grid of $h$ rows and $w$ columns. The rows of the grid are numbered $1$ to $h$ from top to bottom, and the columns of the grid are numbered $1$ to $w$ from left to right. Each row contains exactly one locked sliding wall. Initially, the wall in the $i$-th row spans columns $l[i]$ to $r[i]$ ($1$-indexed), and can be unlocked for $c[i]$ dollars. Once unlocked, it can be slid horizontally to any position along the $i$-th row, as long as it is aligned to the edges of the grid. No part of the wall can leave the left or right edges of the toy. Each column contains a downward-facing laser positioned at the top of the column. If any sliding wall is contained in the $i$-th column, it will block the path of the laser in the $i$-th column. 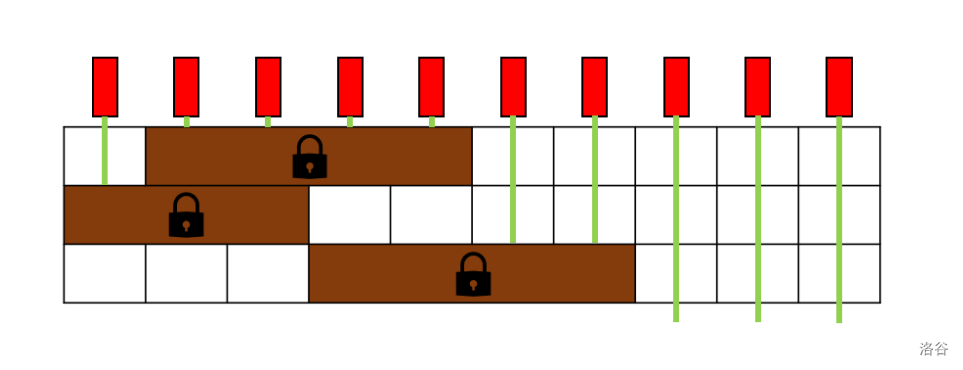A possible toy with $h = 3$ and $w = 10$ is depicted in the diagram below:  Given a total budget of $k$ dollars, Pavement aims to maximise the number of lasers that are not blocked after optimally unlocking and sliding the walls. Determine the maximum number of unblocked lasers he can achieve.

Your program must read from standard input. The first line of input contains three space-separated integers $h, w$ and $k$, describing the number of rows, the number of columns and the budget, respectively. The next $h$ lines of input each contain three space-separated integers. The $i$-th of these lines contains $l[i], r[i]$, and $c[i]$, describing the sliding wall in the $i$-th row.

Your program must print to standard output. Output a single integer, the maximum number of unblocked lasers achievable.

### Subtasks For all testcases, the input will satisfy the following bounds: - $1 \leq h, w \leq 2000$ - $0 \leq k \leq 10^9$ - $1 \leq l[i] \leq r[i] \leq w$ for all $1 \leq i \leq h$ - $0 \leq c[i] \leq 10^9$ for all $1 \leq i \leq h$ Your program will be tested on input instances that satisfy the following restrictions: | Subtask | Marks | Additional constraints | | :-: | :-: | :-: | | $0$ | $0$ | Sample test cases | | $1$ | $6$ | $k = 0, c[i] = 10^9$ | | $2$ | $9$ | $l[i] = r[i]$ | | $3$ | $10$ | $h, w \leq 18$ | | $4$ | $7$ | $h, w \leq 100, k \leq 2000$ | | $5$ | $15$ | $h, w \leq 100$ | | $6$ | $23$ | $h, w \leq 500$ | | $7$ | $8$ | $r[1] − l[1] = r[2] − l[2] = \ldots = r[h] − l[h]$ | | $8$ | $22$ | No additional constraints | ### Sample Test Case 1 Explanation This test case is valid for subtasks $3, 4, 5, 6$, and $8$. The laser toy in the above figure corresponds to this test case. Pavement can unlock the first and second sliding walls for a total cost of $9 + 1 = 10$ dollars. He can then slide the first sliding wall such that it spans columns $4$ to $7$, and slide the second sliding wall to span columns $5$ to $7$.  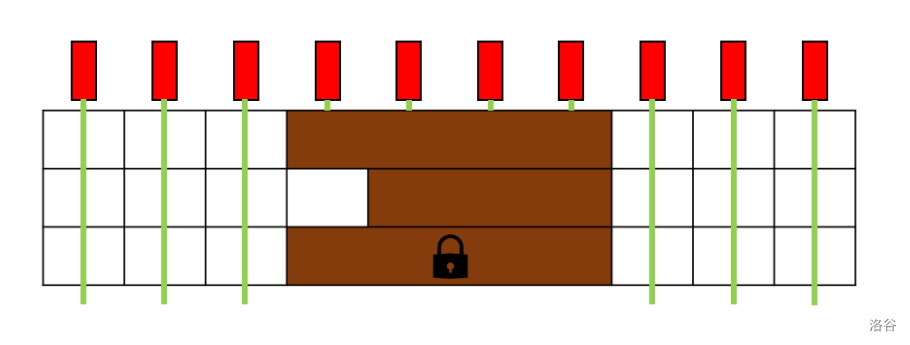This leaves $6$ lasers (in columns $1, 2, 3, 8, 9$, and $10$) unblocked, which is the maximum possible. ### Sample Test Case 2 Explanation This test case is valid for subtasks $2$ to $8$. ### Sample Test Case 3 Explanation This test case is valid for subtasks $1, 3, 4, 5, 6$, and $8$.