P1219 [USACO1.5] Eight Queens Checker Challenge

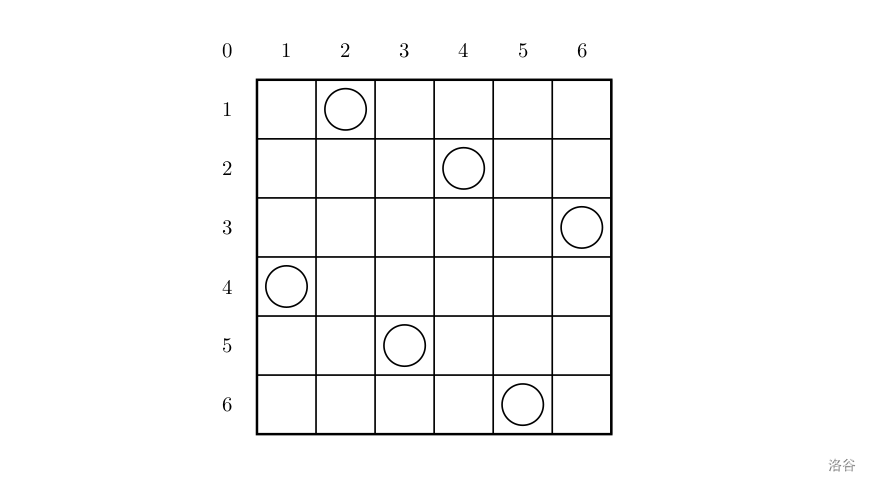
On a $6 \times 6$ checkerboard, six pieces are placed so that there is exactly one in each row and each column, and at most one on each diagonal (including all lines parallel to the two main diagonals).  The layout above can be described by the sequence $2\ 4\ 6\ 1\ 3\ 5$, where the $i$-th number indicates that there is a piece in row $i$ at the corresponding position, as follows: Row numbers $1\ 2\ 3\ 4\ 5\ 6$ Column numbers $2\ 4\ 6\ 1\ 3\ 5$ This is just one solution. Write a program to find all valid placements of the pieces. Output them using the sequence representation above, in lexicographical order. Output the first $3$ solutions. The last line is the total number of solutions.

One line with a positive integer $n$, indicating the board is of size $n \times n$.

The first three lines are the first three solutions; within each solution, separate the numbers with a single space. The fourth line contains a single number, which is the total number of solutions.

Constraints For $100\%$ of the testdata, $6 \le n \le 13$. Problem translation is from NOCOW. USACO Training Section 1.5. Translated by ChatGPT 5