P12305 [ICPC 2023 WF] 骰子已被掷下

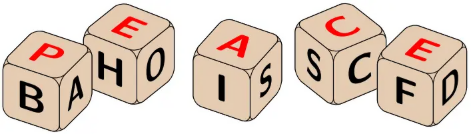
> 译者注：标题原文为 [*Alea Iacta Est*](https://en.wikipedia.org/wiki/Alea_iacta_est)，常被译作「破釜沉舟」，「木已成舟」等。本题题目取其掷骰子的本意。 你正在用一些六面公平骰子玩游戏。骰子的每个表面有一个符号。游戏的目的是掷出骰子并根据每个骰子上面的符号组成一个合法的单词。如果不能组成一个单词，可以重新掷骰子再试一次。  图 K.1. 样例 1 中形成合法单词的五个骰子 假设有五个骰子：其中一个包含字母 `A`、`B`、`C`、`D`、`E` 和 `P`（简写为 `ABCDEP`），其他骰子包含字母 `AEHOXU`、`AISOLR`、`ABCDEF` 和 `ABCSCC`。第一次掷骰子时，骰子朝上的面会出现以下字母：`P`、`X`、`R`、`E` 和 `S`。由于无法将这些字母组合成一个合法的单词，你决定保留 `P`、`S` 和 `E`，重新掷其他骰子，试图组成 `PARSE`、`PAUSE`、`PHASE`、`POISE`、`PROSE`、`PULSE` 或 `PURSE` 等单词。重新掷两颗骰子，分别掷出 `E` 和 `A`，得到以下五个字母：`P`、`E`、`A`、`E` 和 `S`。你仍然想不到一个合法的单词，于是决定保留四个字母，只重新掷最后一个骰子，该骰子三面都是字母 `C`。如图 K.1 所示，这样做有 $50\%$ 的几率可以得到一个最终有效的单词：`PEACE`。 当你掷骰子时，骰子每个面朝上的概率相等。假定使用最优策略，那么掷出一个合法单词所需的期望掷骰次数是多少？

第一行输入包含两个数字 $d$ 和 $w$，其中 $d$（$1 \le d \le 6$）是骰子的个数，$w$（$1 \le w \le 2\cdot 10^5$）是字典中合法单词的个数。接下来 $d$ 行每行有 $6$ 个符号，表示骰子的每个面上的符号。最后的 $w$ 行包含字典中 $w$ 个互不相同的合法单词。每个单词恰好包含 $d$ 个符号。 输入中所有符号要么是大写英文字母（`A-Z`），要么是数字（`0-9`）。

如果有可能掷出一个合法单词，则输出使用最优策略掷出一个合法单词所需的期望掷骰次数。否则，输出 `impossible`。输出与答案的绝对或相对误差应不超过 $10^{-6}$。