P12311 [ICPC 2022 WF] Archaeological Recovery

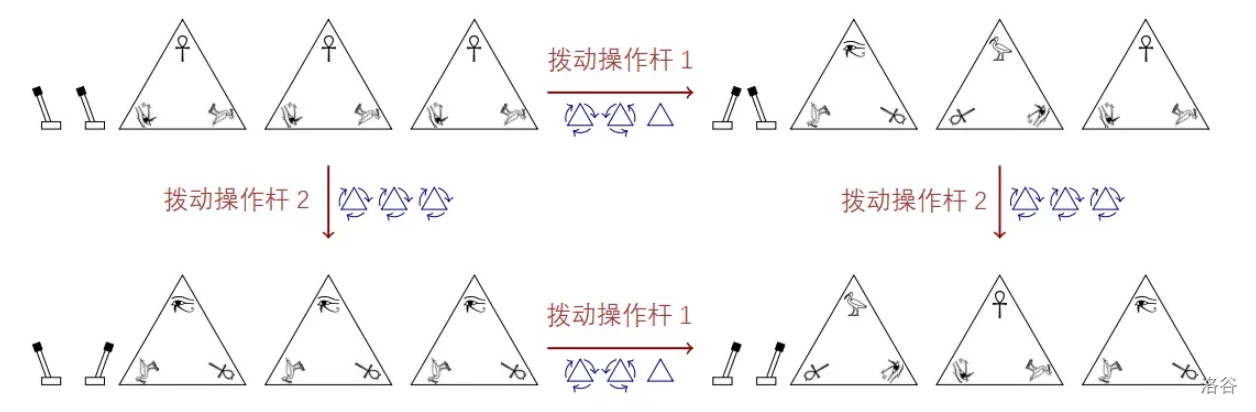
著名的埃及学教授 Z Mummer 正在卢克索新发现的墓室中探索，在其中她发现了一个神秘的构造。在墙上，有一排 $k$ 个金字塔形的石板。每块石板上都有三个象形文字：生命之符（上部），荷鲁斯之眼（左下部）以及朱鹮（右下部）。 在墙边有 $n$ 个操纵杆。教授小心地试验这些操纵杆，警惕潜在的陷阱，她发现每个操纵杆都可以使某些石板顺时针或逆时针旋转，使另一个象形文字位于上部。回拨操纵杆可以使相同的石板以相反的方向旋转回到原位。这些操纵杆是完全独立的，因此无论其他操纵杆的状态如何，拨动或回拨某个操纵杆都会产生相同的效果。见图 Z.1 示意图。  图 Z.1 展示了一堵有 3 个金字塔石板和 2 个操纵杆的墙。第一个操纵杆使第一个金字塔顺时针旋转，第二个金字塔逆时针旋转，第三个金字塔保持不变。第二个操纵杆使三个金字塔都顺时针旋转。这对应样例 1。 出于好奇，Mummer 教授记录了每个操纵杆各自的效果。回到大学后，她让一名学生干了一件体力活：对于所有 $2^n$ 种可能的操作杆状态，找出所有石板可能的排布情况（其中一些可能相同），以便进一步研究。 经过很多天的精心计算，学生终于完成了任务，开始整理资料。但灾难随即发生：他不小心打翻了墨水，完全毁坏了教授最初的笔记，这些笔记是记录每个操纵杆各自效果的唯一记录。 避免 Mummer 教授生气的唯一机会就是从可能的石板排布列表重建原始笔记。这无法完全无歧义地进行（例如，无法区分同一组操纵杆的不同操作顺序）。但只要根据复原的笔记仍然能计算出石板的排布情况，这种错误就不太可能被发现（至少在这个学生毕业之前不会被发现）。

第一行包含三个整数 $n,k,t$。其中 $n$（$1\le n\le 40$）和 $k$（$1\le k\le 5$）分别为操纵杆数和金字塔形石板数，$t$（$1\le t\le 3^k$）表示不同的石板排布状态数。接下来 $t$ 行描述这些互不相同的石板排布状态。首先一个长为 $k$ 的字符串，描述这个状态，然后一个整数 $f$（$1\le f\le 2^n$）表示有多少种操纵杆状态可以使石板达到这个状态。石板状态用 `A`，`E` 和 `I` 三种字母表示。第 $j$ 个字母表示第 $j$ 个石板上朝上的象形文字：`A` 表示生命之符，`E` 表示荷鲁斯之眼，`I` 表示朱鹮。 这 $t$ 个状态两两不同，所有状态的 $f$ 值相加等于 $2^n$，输入中至少存在一组操纵杆能产生给定的多组状态。

输出 $n$ 行描述一组可能得到给定石板排布数的操纵杆配置。每行用 $k$ 个字符 `+`，`-` 或 `0` 描述一个操纵杆。每个字符串中的第 $j$ 个字符描述这个操纵杆对第 $j$ 个石板的影响：如果让石板顺时针旋转，则为 `+`，如果让石板逆时针旋转，则为 `-`，如果让石板保持不动，则为 `0`。 如果有多种可能的答案，输出任意一种均可。