P1232 [NOI2013] Counting Trees

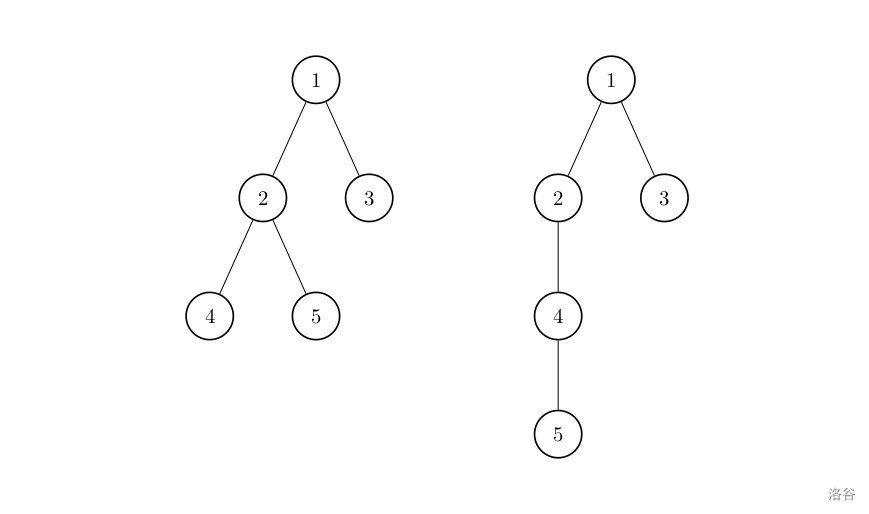
We know that a rooted tree can be traversed by depth-first search (DFS) and breadth-first search (BFS) to generate the DFS order and BFS order of the tree. Two different trees may have the same DFS order, and they may also have the same BFS order. For example, the two trees below both have DFS order `1 2 4 5 3` and BFS order `1 2 3 4 5`.  Given a DFS order and a BFS order, we want to know the average height of all rooted trees that satisfy them. That is, suppose there are $K$ different rooted trees that have this pair of DFS and BFS orders, and their heights are $h_1, h_2, \ldots, h_K$. Please output: $$ \frac{h_1+h_2+\ldots+h_K}K $$

The first line contains $1$ positive integer $n$, the number of nodes of the tree. The second line contains $n$ positive integers, a permutation of $\,$ $1 \ldots n$, representing the DFS order of the tree. The third line contains $n$ positive integers, a permutation of $\,$ $1 \ldots n$, representing the BFS order of the tree. It is guaranteed that there exists at least one tree consistent with the given two sequences.

Output $1$ real number, rounded to exactly three decimal places, representing the average tree height.

If the absolute difference between your output and the standard answer does not exceed $0.001$, you will receive full credit for that test point; otherwise, you will receive no credit. Constraints - For $20\%$ of the testdata: $n \le 10$. - For $40\%$ of the testdata: $n \le 100$. - For $85\%$ of the testdata: $n \le 2 \times 10^3$. - For $100\%$ of the testdata: $2 \le n \le 2 \times 10^5$. Translated by ChatGPT 5