P12362 [eJOI 2024] 霍拉舞 / Hora

**这是一道交互题！** **特别提醒：本题为 0-indexed。** **为了适配洛谷评测机，本题改用 IO 交互。**

在第 $8$ 届 eJOI 举行之际，$N$ 位选手正围成一圈跳霍拉舞！这里，$N$ 是一个正偶数，且这 $N$ 名选手中男女人数相同。组织者为每名选手分配了一个编号，从 $0$ 到 $N-1$。编号是顺着分配的，也就是说，$i$ 与 $i-1$ 和 $i+1$ 相邻；特别的，$0$ 与 $1$ 和 $N-1$ 相邻。 你并不知道哪些选手是男生，哪些选手是女生。但是，由于你正在比赛中，所以你只能向评测机问问题！在一次问题中，你可以给两个整数 $L$ 和 $R$，保证 $0 \le L,R < N$，然后： - 如果 $L\le R$，评测机会返回 $[L,R]$ 中男生的数量。 - 否则，评测机会返回 $[L,N-1]$ 和 $[0,R]$ 中总共男生的数量。 给你一个 $K$，现在，你需要通过询问评测机若干个如上问题，来找到这个环中长度为 $K$ 的一段，使得这一段中男生和女生人数差最小。你需要输出在圆上连续的这一段的起点 $S$。如果有多个这样的 $S$，你可以输出任意一个。

无

无

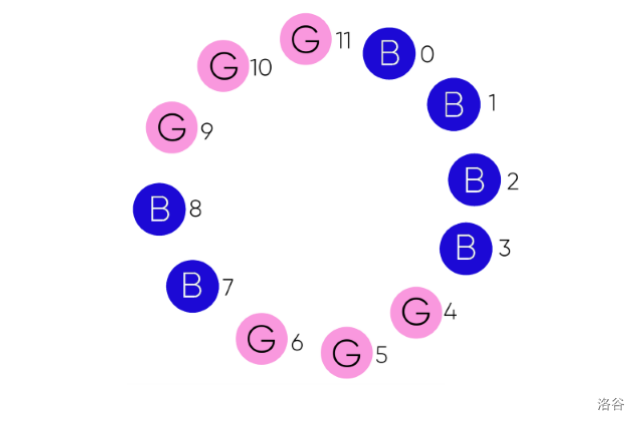
**【样例解释】** 排列如下：  其中一种正确答案是 $1$，因为 $[1,5]$ 中有 $3$ 男 $2$ 女，差为 $3-2=1$，为最小。 **【数据范围】** 对于 $100\%$ 的数据，$2 \le N \le 10^5$，$N$ 为偶数，$1 \le K \le N$，交互库不自适应（即，男女生的分布在一开始就已经确定，不会改变）。 |$\text{Subtask}$|分值|特殊性质|$Q_{full}$| |:-:|:-:|:-:|:-:| |$1$|$5$|$N=34$|$34$| |$2$|$13$|$N=100000$，所有男孩都相邻|$18$| |$3$|$8$|$N=100000$，数据随机|$34$| |$4$|$11$|$N=100000,K=50000$|$18$| |$5$|$10$|$N=65536,K=128$|$26$| |$6$|$10$|$N=100000,K=400$|$26$| |$7$|$9$|$N=100000,K=99601$|$26$| |$8$|$10$|$N=100000,K=330$|$68$| |$9$|$24$|无|$34$| **【计分方式】** 在每一个 $\text{Subtask}$ 中都有 $Q_{full}$ 和分值。假设在你一共询问了 $Q$ 次。 - 如果 $Q\le Q_{full}$ 你就可以得到该测试点的全部分数。 - 如果 $N\ge Q\ge Q_{full}$ 那么你可以得到分值 $\times\Bigg(1-\Bigg(\dfrac{(Q-Q_{full})}{N}\Bigg)^{0.05}\Bigg)$ 分。 - 如果 $Q>N$ 那么你不得分。 一个 $\text{Subtask}$ 的得分是其所有测试点的得分最小值。