P12375 「LAOI-12」MST?
题目背景

题目描述
给定 $n,m$ 两个正整数,构造无重边**无自环**的一张连通无向图,共 $n$ 个结点和 $m$ 条边权分别为 $1\sim m$ 的边,使得其最小生成树的边权和最大。
你只需要输出最小生成树的边权和对 $998244353$ 取模的值即可。
输入格式
**本题有多组测试数据。**
第一行输入一个正整数 $T$,表示测试数据组数。
对于每组测试数据,共一行两个正整数 $n,m$。
输出格式
共 $T$ 行,对于每组数据输出最小生成树的边权和对 $998244353$ 取模的值即可。
说明/提示
### 样例解释
对于样例一中的第一组测试数据,构造如下:
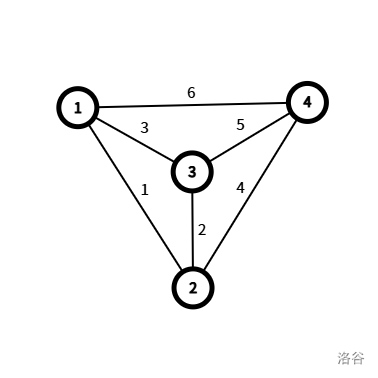
此时答案为 $1+2+4=7$。
### 数据范围
**本题采用捆绑测试。**
|子任务编号|$T$|$n$|特殊性质|分值|
|:-:|:-:|:-:|:-:|:-:|
|$1$|$\le5$|$\le5$|无|$5$|
|$2$|$\le10^6$|$\le10^3$|无|$10$|
|$3$|$\le5$|$\le10^6$|无|$15$|
|$4$|$\le10^6$|$\le10^6$|无|$20$|
|$5$|$\le10^6$|$\le10^{18}$|$n=m$|$5$|
|$6$|$\le10^6$|$\le10^{18}$|无|$45$|
对于 $100\%$ 的测试数据,满足 $1\le T \le 10^6$,$4\le n\le m\le 10^{18}$,$m\le \frac{n\times(n-1)}{2}$。