P1240 Placement of Feudal Lords

A long time ago, there was a powerful empire whose territory was square-shaped, as shown in the figure. The country has several feudal lords. Since these lords had made great contributions, the king planned to grant each of them a fief (one cell in the square grid). However, these lords are very warlike: if two lords are in the same row or the same column, they will go to war. The following figure shows the territory when $n=3$, where the shaded cells indicate the lords’ positions. In the first two figures, the lords can attack each other; in the third figure, they cannot.  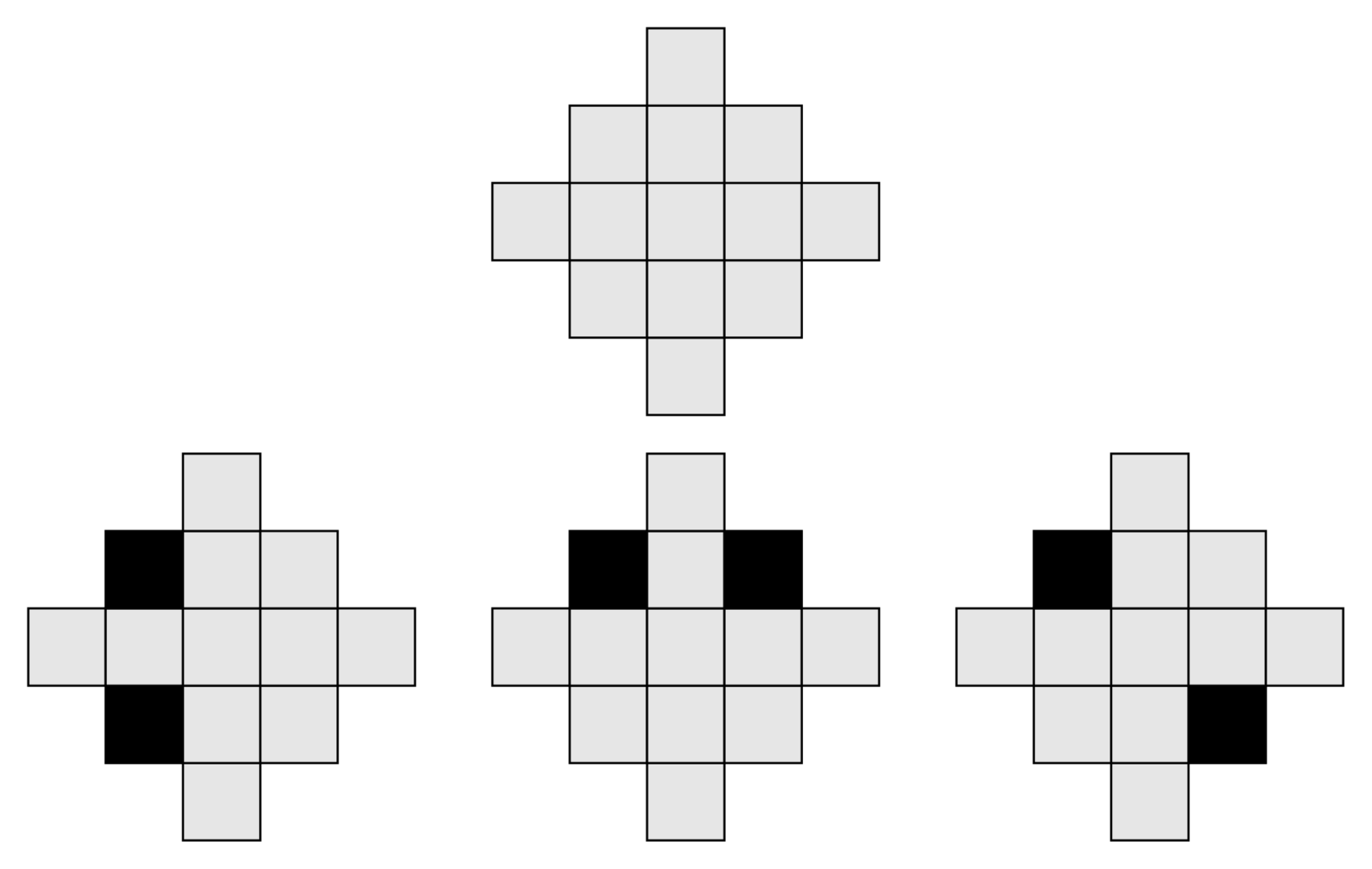Naturally, the king does not want to see his lords fighting each other and causing unrest. Therefore, he hopes to arrange their positions so that no two lords can attack each other. Now, given the side length $n$ of the square and the number of lords $k$ to be placed, find the total number of valid arrangements. (You only need to output the remainder when the number of arrangements is divided by $504$.) Constraints: $n \le 100$, $k \le 2n^2 - 2n + 1$.

A single line containing two integers $n$ and $k$, separated by a space.

A single integer, the remainder when the number of valid arrangements is divided by $504$.

Note: Mirror images and rotations are considered different solutions. Translated by ChatGPT 5