P12415 「YLLOI-R1-T4」枫


有一个 $n$ 行 $m$ 列的网格，你要在该网格上制造一棵树，要求： - 该树的每个节点对应一个格子。 - 每个格子最多对应一个节点。 - 该树任意节点对应格子所处行数小于其任意儿子节点对应格子所处行数。（行数从上往下严格递增） 节点没有编号，即所有节点是相同的。 定义两棵树相同需满足的所有条件： - 总节点数相同。 - 对应节点都位于同一格子。形式化地，设两棵树所有节点对应格子的集合分别为 $S_1,S_2$，则 $S_1=S_2$。 - 对应节点所有父子关系均相同。形式化地，使用 $x$ 表示一个格子，则 $\forall x\in S_1,S_2$，设其对应节点的儿子节点对应格子的集合分别为 $S_1{'},S_2{'}$，则 $S_1{'}=S_2{'}$。 问一共能制造出多少种不同的树，答案对 $10^9+7$ 取模。

无

无

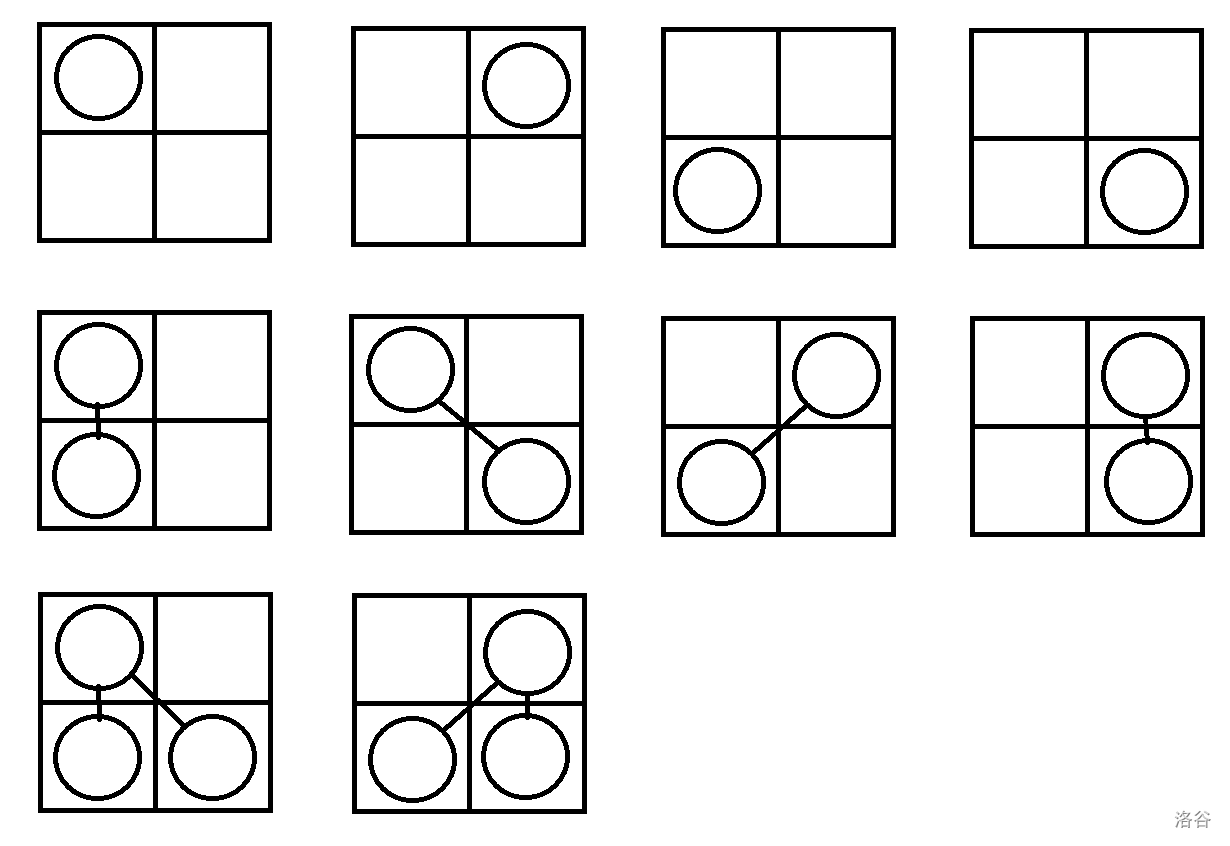
#### 【样例解释#1】 下图为所有不同的树：  #### 【样例解释#2】 - 共有 $6$ 种不同的 $1$ 个节点的树。 - 共有 $12$ 种不同的 $2$ 个节点的树。 - 共有 $22$ 种不同的 $3$ 个节点的树。 - 共有 $28$ 种不同的 $4$ 个节点的树。 - 共有 $18$ 种不同的 $5$ 个节点的树。 - 共有 $0$ 种不同的 $6$ 个节点的树。 因此共有 $6+12+22+28+18+0=86$ 种不同的树。 #### 【数据范围】 **本题采用捆绑测试。** - Subtask 1（10 pts）：$n=2$。 - Subtask 2（10 pts）：$m=1$。 - Subtask 3（10 pts）：$n,m \le 3$。 - Subtask 4（20 pts）：$n,m \le 20$。 - Subtask 5（20 pts）：$n,m \le 50$。 - Subtask 6（30 pts）：无特殊限制。 对于全部数据，保证：$1\le n,m\le80$。