P12415 「YLLOI-R1-T4」 Maple


There is a grid with $n$ rows and $m$ columns. You need to construct a tree on this grid such that: - Each node of the tree corresponds to a cell in the grid. - Each cell can correspond to at most one node. - For any node in the tree, the row of its corresponding cell is strictly less than the row of any of its children. (Rows are numbered from top to bottom.) The nodes are unlabelled; all nodes are identical. Two trees are considered identical if they satisfy all the following conditions: - They contain the same number of nodes. - The set of grid cells corresponding to the nodes are the same. Formally, if the set of cells used in the two trees are $S_1$ and $S_2$, then $S_1 = S_2$. - The parent–child relationships are exactly the same. Formally, for every cell $x\in S_1,S_2$, let $S_1'$ and $S_2'$ be the sets of cells corresponding to the children of $x$ in the two trees,then $S_1'=S_2'$. Determine how many distinct trees can be constructed. Output the answer modulo $10^9 + 7$.

A single line containing two positive integers $n$ and $m$.

A single integer — the number of distinct trees modulo $10^9 + 7$.

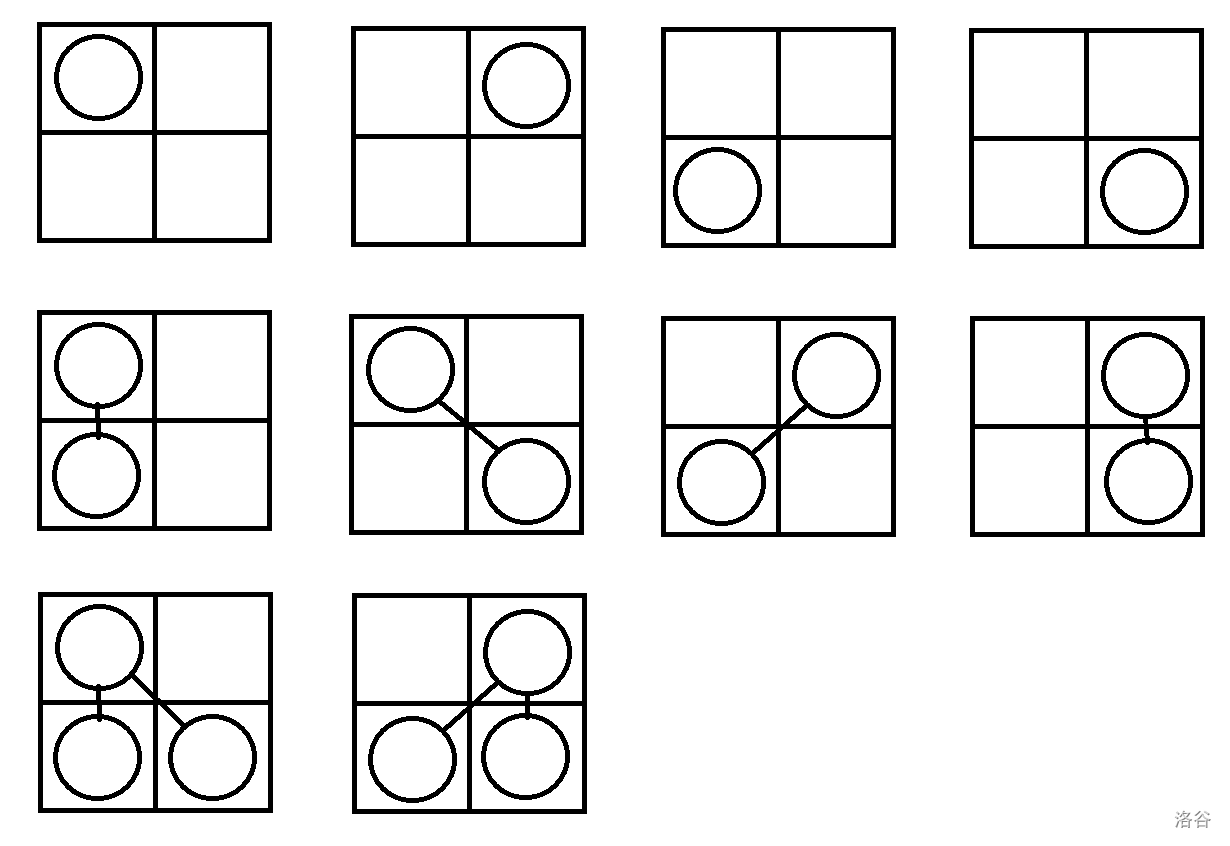
### Explanation **Sample 1:** The figure below shows all distinct trees:  **Sample 2:** - There are $6$ distinct trees with $1$ node. - There are $12$ distinct trees with $2$ nodes. - There are $22$ distinct trees with $3$ nodes. - There are $28$ distinct trees with $4$ nodes. - There are $18$ distinct trees with $5$ nodes. - There are $0$ distinct trees with $6$ nodes. So in total, there are $6 + 12 + 22 + 28 + 18 + 0 = 86$ distinct trees. ### Constraints **This problem uses subtask scoring.** - Subtask 1 (10 pts): $n = 2$. - Subtask 2 (10 pts): $m = 1$. - Subtask 3 (10 pts): $n, m \le 3$. - Subtask 4 (20 pts): $n, m \le 20$. - Subtask 5 (20 pts): $n, m \le 50$. - Subtask 6 (30 pts): No additional constraints. For all data: $1 \le n, m \le 80$.