P12418 【MX-X12-T1】「ALFR Round 5」地铁

原题链接：。

为了方便市民出行，缓解地面上的道路拥堵问题，S 市决定在地底下建一些地铁。 根据城市规划，S 市的地下网络将由 $n$ 条横向通道和 $m$ 条纵向通道构成。地铁站将设置在所有横向通道与纵向通道的交叉处，共 $n\times m$ 处。 地下网络的所有站点都需要被地铁线路覆盖，地铁线路之间可以有重叠部分。 由于地铁拐弯处的建造成本、安全要求较高，因此，S 市要求**每一条地铁线路途径的所有站点，均在同一条横向通道或纵向通道内**。即，地铁线路不能拐弯。 此外，地铁线路网必须是连通的。也就是说，无论从哪个地铁站出发乘坐地铁，经过若干次换乘（可以不换乘），都一定可以到达其它所有地铁站。 例如，当 $n=5$，$m=7$ 时，下图就是一个符合 S 市要求的地铁交通网络图（灰线代表地下通道，深灰色的格子为地铁站，即道路交叉处）。  因为盾构一条地铁线路的流程十分麻烦，S 市不想要建造太多的地铁线路。现在，你知道了 S 市的地下网络大小为 $n\times m$，请你求出 S 市最少要建几条地铁线路。

无

无

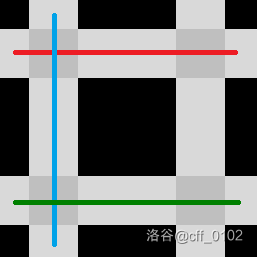
**【样例解释】** 在第一组数据中，需要建造一条长度为 $0$，经过唯一一个站点的地铁线路。 在第二组数据中，需要建造一条长度为 $1$，连接两个站点的地铁线路。 在第三组数据中，一个合法的建造方案如下图。要覆盖所有深灰色的交叉路口，至少需要三条地铁线路。  **【数据范围】** 对于 $15\%$ 的数据，保证 $n=1$。 对于另外 $15\%$ 的数据，保证 $n,m\le10$。 对于另外 $15\%$ 的数据，保证 $n=m$。 对于另外 $15\%$ 的数据，保证 $n\le m$。 对于 $100\%$ 的数据，$1\le T\le10$，$1\le n,m\le3\times10^4$。