P12427 [BalticOI 2025] Tour

托伦有许多旅游景点。我们的导游准备了一份包含 $m$ 条单向步行路线的清单，这些路线连接了市中心的 $n$ 个集合点。步行路线编号为 1 到 $m$，集合点编号为 1 到 $n$。每条步行路线从一个集合点出发，到达另一个集合点，途中可以参观一个景点。不同的步行路线可能参观相同的景点，并且同一对集合点之间可能存在多条步行路线。我们希望在休息日组织一次**有趣的游览**。 一次**游览**是指一系列步行路线，其中每条步行路线的起点是前一条步行路线的终点。此外，最后一条步行路线的终点必须是最初第一条步行路线的起点。 如果一次游览中不会连续两次参观相同的景点，则称其为**有趣的游览**。换句话说，游览中任意两条连续的步行路线参观的景点必须不同，并且第一条和最后一条步行路线参观的景点也必须不同。注意，我们不关心非连续的步行路线是否参观相同的景点。特别地，同一条步行路线可以在游览中多次使用（但不能连续使用两次）。 你的任务是判断是否可以组织一次**有趣的游览**，如果可以，则找到一条这样的游览。你可以输出任意一条包含不超过 $m$ 条步行路线的有趣游览。可以证明，如果存在有趣的游览，那么一定存在一条不超过 $m$ 条步行路线的有趣游览。

第一行包含一个正整数 $t$（$1 \leq t \leq 5 \cdot 10^5$），表示测试用例的数量。 每个测试用例的第一行包含两个正整数 $n$ 和 $m$（$2 \leq n$，$1 \leq m$），分别表示集合点的数量和步行路线的数量。 接下来的 $m$ 行描述了 $m$ 条步行路线。第 $i$ 行包含三个正整数 $x_i$、$y_i$ 和 $c_i$（$1 \leq x_i, y_i \leq n$，$x_i \neq y_i$，$1 \leq c_i \leq m$），表示第 $i$ 条步行路线从集合点 $x_i$ 出发，到达集合点 $y_i$，并且参观的景点编号为 $c_i$。 设 $N$ 和 $M$ 分别表示所有测试用例中 $n$ 和 $m$ 的总和。你可以假设 $N, M \leq 10^6$。

对于每个测试用例，第一行输出 YES 表示可以组织有趣的游览，否则输出 NO。如果可以组织，则在第二行首先输出一个正整数 $k$（$2 \leq k \leq m$），表示构成有趣游览的步行路线数量。随后输出 $k$ 个用单个空格分隔的整数 $p_1, p_2, \ldots, p_k$，这些数字描述了一条有趣的游览，其中我们首先走步行路线 $p_1$，然后是 $p_2$，依此类推，最后走步行路线 $p_k$ 回到最初的集合点。

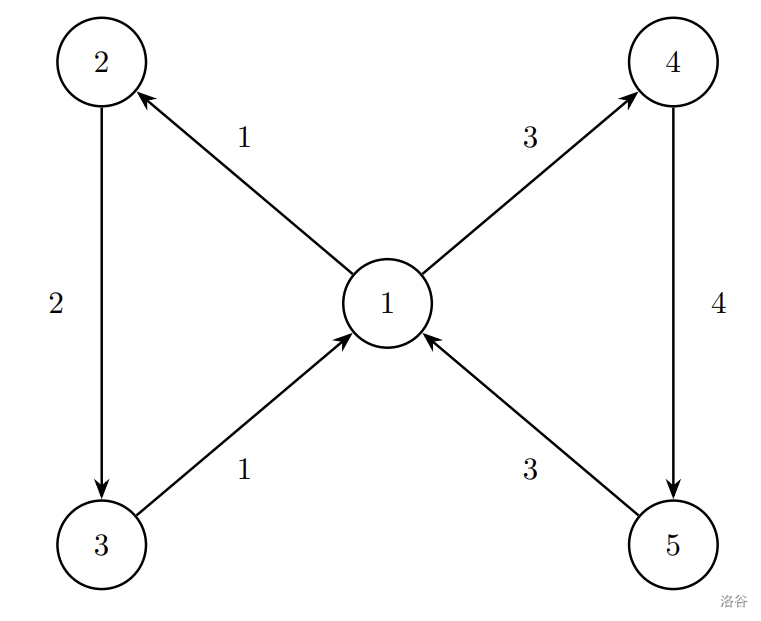
 示例中第 4 个测试用例的图示。箭头表示集合点之间的步行路线。 ### 评分 | 子任务 | 限制条件 | 分值 | | :---: | :---: | :---: | | 1 | $m \leq 10$ 且 $t \leq 100$ | 9 | | 2 | $M \leq 5000$ | 23 | | 3 | $M \leq 5 \cdot 10^4$ | 19 | | 4 | $M \leq 2 \cdot 10^5$ | 25 | | 5 | 无额外限制。 | 24 | 翻译由 DeepSeek V3 完成