P12428 [BalticOI 2025] Tower

关于托伦斜塔有许多传说。塔的墙壁是一个带有 $N \geq 3$ 个均匀分布的门（换句话说，这些门构成一个正 $N$ 边形的顶点）的圆形结构。门的编号从 0 到 $N - 1$，但顺序是随机的。更多细节请参考评分部分。 其中一个不太为人所知的传说描述了每位新居民必须完成的挑战。挑战的目标是列出所有门，从某一扇门开始，然后沿着圆形（顺时针或逆时针）行走，恰好访问每扇门一次。 这一过程无法直接观察塔楼，而是需要通过提问来获取信息。每次提问的形式如下："给定三扇不同的门 $x$、$y$、$z$，哪对门之间的距离最近：$\{x, y\}$、$\{y, z\}$ 还是 $\{z, x\}$？"。这类问题的回答将给出所有距离最近的门对（在 $\{x, y\}$、$\{y, z\}$ 和 $\{z, x\}$ 中）。距离是指连接两扇门的最短线段的长度。你的任务是编写一个程序，通过少量此类提问来确定门的排列顺序。 ### 交互说明 这是一个交互式任务。你需要编写一个程序，通过与交互器进行标准输入输出的交互来解决问题。 在交互开始时，你的程序应从标准输入读取两个整数 $t$ 和 $k$（$1 \leq t \leq 100$，$1 \leq k \leq 12000$），分别表示测试用例的数量和允许的平均提问次数上限。更多信息请参考评分部分。 对于每个测试用例，你的程序应首先从标准输入读取一个整数 $n$（$3 \leq n \leq 500$），表示塔楼中门的数量。 然后，你的程序可以通过以下方式提问： - 向标准输出写入一行格式为 $?\ x\ y\ z$ 的内容，其中 $x$、$y$ 和 $z$ 是不同的整数（$0 \leq x, y, z \leq n - 1$）。这一行表示一个关于门 $x$、$y$ 和 $z$ 的提问。 - 交互器的响应格式为： $r$ $a_1\ b_1$ $\vdots$ $a_r\ b_r$ 其中 $r$ 是一个整数（$1 \leq r \leq 3$），表示距离最近的门对数量。每个门对由两个整数 $a_i$ 和 $b_i$（$a_i, b_i \in \{x, y, z\}$ 且 $a_i < b_i$）描述。 一旦确定了门的顺序，你的程序应向标准输出写入一行格式为 $!\ x_0\ x_1\ \dots\ x_{n-1}$ 的内容，其中 $x_0, x_1, \ldots, x_{n-1}$ 是题目描述中要求的门的顺序。注意共有 $2n$ 种可能的正确答案，因为你可以从任意一扇门开始，并按任意方向排列。其中任何一种都会被接受。 **请记住，每次提问或回答后，必须使用 `cout.flush()`（或 `fflush(stdout)`，如果使用 `printf`）或 Python 中的 `sys.stdout.flush()` 刷新输出缓冲区。** 否则你的程序可能会因超时而失败。 在向交互器输出答案后，你的程序应立即处理下一个测试用例，或在所有测试用例处理完毕后结束交互。 你的程序不能打开任何文件或使用其他资源。可以使用标准错误流进行调试，但请注意写入该流会消耗时间。 另外请注意，交互器不是自适应的，即每个测试用例中门的初始顺序在交互开始前已固定，不会在交互过程中改变。

参见交互说明。

参见交互说明。

假设我们只有一个测试用例，$n = 6$，且门的顺序为 $5, 3, 0, 2, 1, 4$。交互过程可能如下： | 交互器 | 你的程序 | 说明 | | :---: | :---: | :---: | | 1 100 | | $t=1$ 且 $k=100$。 | | 6 | | 交互器给出第一个测试用例的门数。 | | | ? 0 1 2 | 你的程序询问哪对门距离最近。 | | 2 | | 门对 $\{0,2\}$ 和 $\{1,2\}$ 距离最近。 | | 0 2 | | | | 1 2 | | | | | ? 4 1 3 | 你的程序询问哪对门距离最近。 | | 1 | | 门对 $\{1,4\}$ 距离最近。 | | 1 4 | | | | | ? 0 5 1 | 你的程序询问哪对门距离最近。 | | 3 | | 门对 $\{0,5\}$、$\{0,1\}$ 和 $\{1,5\}$ 距离最近。 | | 0 5 | | | | 0 1 | | | | 1 5 | | | | | ! 4 5 3 0 2 1 | 你的程序正确输出门的顺序。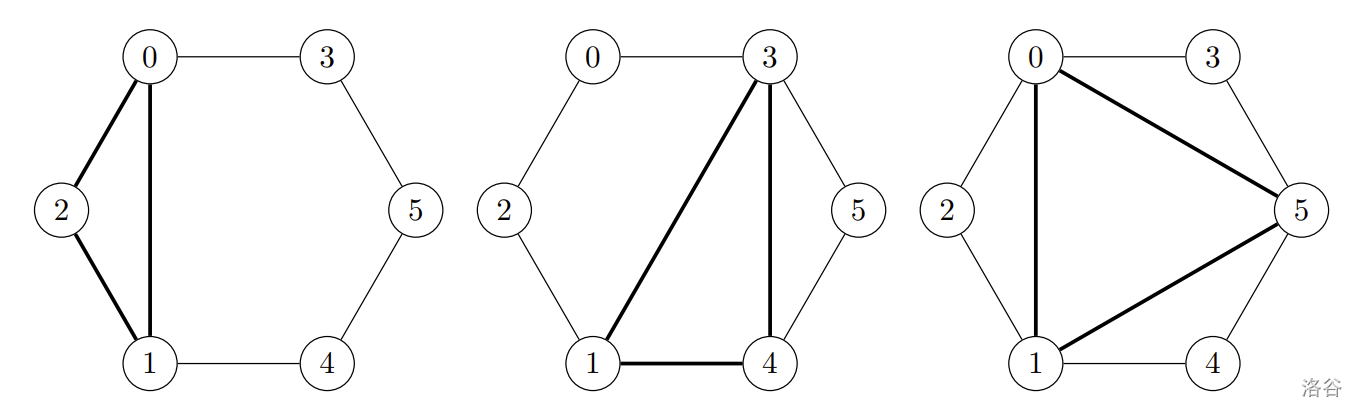 |  样例解释：上图展示了塔楼墙壁上门的编号。最左边的图片显示了编号为 $0, 1, 2$ 的门形成的三角形，对应你的程序的第一个提问。可以看到，门对 $\{0, 2\}$ 和 $\{1, 2\}$ 距离最近。中间的图片显示了编号为 $1, 4, 3$ 的门形成的三角形，对应第二个提问。显然，门对 $\{1, 4\}$ 距离最近。最右边的图片显示了编号为 $0, 1, 5$ 的门形成的三角形，对应第三个提问。可以看到，所有门对的距离都相等。 注意，序列 $0, 2, 1, 4, 5, 3$ 或 $5, 4, 1, 2, 0, 3$（以及其他几种）在此情况下也是正确答案。 ### 评分 本题的评分分为多个子任务。每个子任务仅包含一个测试，该测试包含 $t = 100$ 个测试用例。对于每个测试，你的程序的平均提问次数为所有测试用例的总提问次数除以测试用例数。如果该平均值超过给定子任务的 $k$ 值，则该子任务得分为 $0$。否则，对于子任务 1 至 4，你将获得该子任务的满分。 对于最后一个子任务，你的得分将按以下方式计算。设 $k^*$ 为你的程序实际的平均提问次数，则得分由以下公式给出： $$\left\lceil 56 \cdot \min \left(1, \frac{12000 - k^*}{7800}\right) \right\rceil$$ 这意味着当 $k^*$ 从 12000 降到 4200 时，你的得分将从 0 线性增加到 56。 请注意，如果你的程序在任何测试用例中给出错误答案，无论提问次数多少，该子任务的得分都将为 0。 各子任务的额外约束如下表所示： | 子任务 | 约束条件 | 分值 | | :---: | :---: | :---: | | 1 | $k = 8000, 3 \leq n \leq 9$ | 6 | | 2 | $k = 4500, 40 \leq n \leq 50$ | 7 | | 3 | $k = 3000, 90 \leq n \leq 100$ | 9 | | 4 | $k = 4500, n = 400$，存在正确答案 $x_0, \ldots, x_{n-1}$ 满足 $x_i = i$（$200 \leq i \leq 399$） | 22 | | 5 | $k = 12000, n = 500$ | 最高 56 | 此外，可以假设每个测试用例的生成方式为：首先从满足子任务约束的所有 $n$ 值中均匀随机选择一个 $n$，然后从满足子任务约束的所有 $n$ 扇门的排列中均匀随机选择一个顺序。 翻译由 DeepSeek V3 完成