P1244 [NOI2000] Frogs Crossing the River

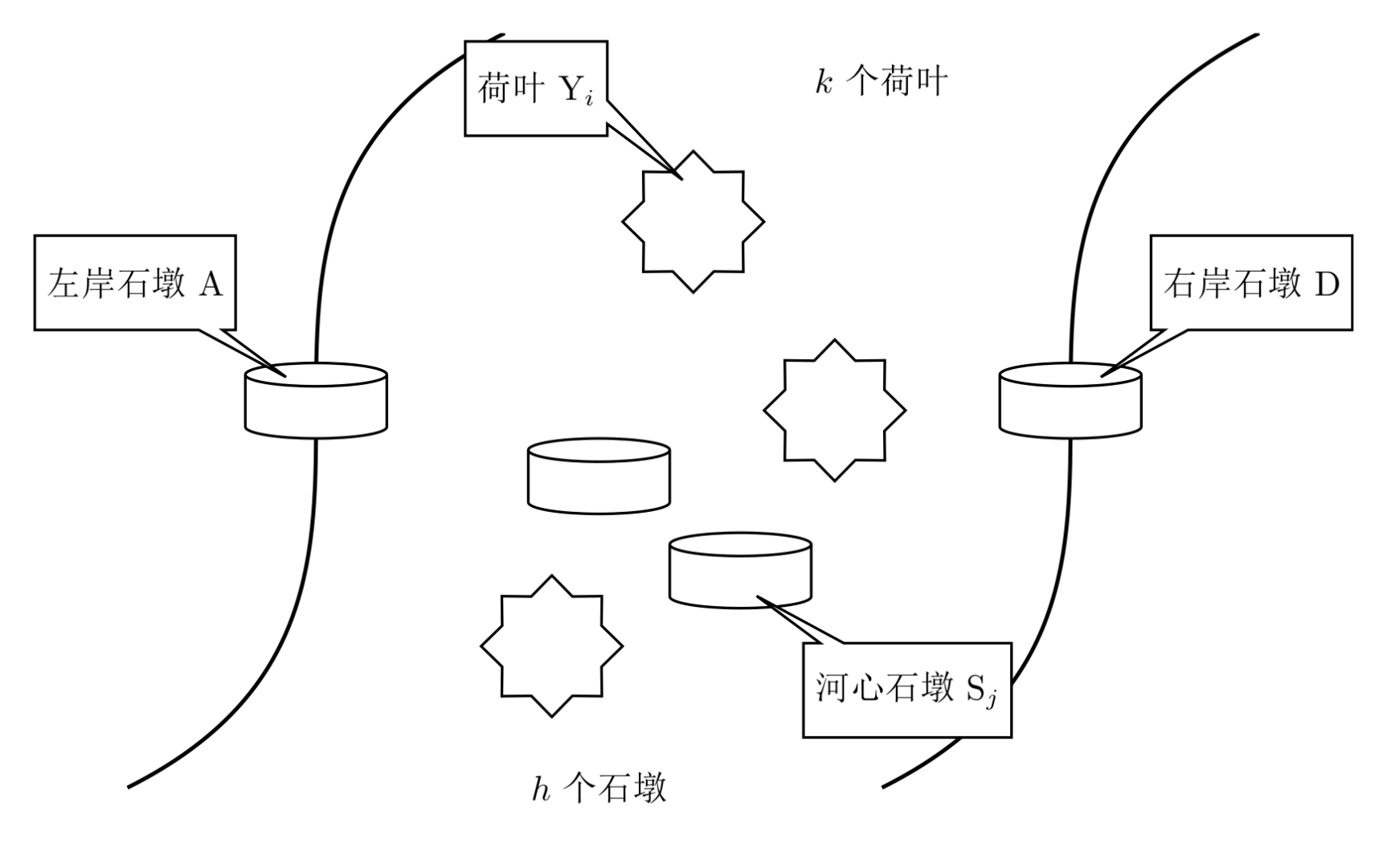
A line of frogs of different sizes stands on the stone post on the left bank (denoted as A) and wants to cross to the stone post on the right bank (denoted as D). There are several lily pads in the middle of the river (denoted as $Y_1 \dots Y_m$) and several stone posts (denoted as $S_1\dots S_n$). The illustration is as follows:  The lineup and movement rules for the frogs are as follows: - Each frog may stand only on a lily pad, a stone post, or on the back of a frog that is only one size larger than itself (collectively called valid landing spots). - A frog can jump from one landing spot to another only when there is no other frog on its back. - A frog is allowed to jump directly from the left bank A to stone posts or lily pads in the river center, as well as directly to the right-bank stone post D; a frog is also allowed to jump from stone posts or lily pads in the river center to the right-bank stone post D. - Frogs may jump back and forth among stone posts, among lily pads, and between stone posts and lily pads in the river center. - After leaving the left bank stone post, a frog cannot return to the left bank; after reaching the right bank, it cannot jump back. - Stone posts have very large load capacity and can hold any number of frogs; however, because their area is small, at most one frog may stand directly on a stone post, and any other frogs must, per Rule 1, stand on the back of a frog that is one size larger. - Lily pads not only have small area but also limited load capacity; at most one frog may stand on a lily pad. - At each step, only one frog may move, and after the move the lineup rules must be satisfied. - Initially, all frogs stand on A: the largest frog stands directly on the stone post, and all other frogs, per Rule 6, stand on the back of a frog that is one size larger. The frogs hope that they can all eventually move onto D and complete the lineup. Given that the river center has $m$ lily pads and $n$ stone posts, determine the maximum possible number of frogs that, under the lineup and movement rules, can move from A to D. Your task is: given $n, m$, compute and output the maximum number of frogs that can cross the river under the rules above.

Two integers $n, m$.

One integer, the maximum number of frogs that can, under the rules above, cross the river from A to D.

Constraints: $n \leq 20$, $m \leq 10^3$. Translated by ChatGPT 5