P12534 [XJTUPC 2025] Ori

The Spirit Tree is the source of life on Nibel Mountain, with its roots flowing with light that maintains the ecological balance of the entire forest. The body of the ancient tree is composed of $n$ cores of light, which are interconnected by $n−1$ energy branches to form an acyclic tree structure. Between any two cores, there is a unique energy branch path winding between them, as if woven by the threads of fate. Ori, originally the guardian spirit nurtured by the ancient tree, was swept into the abyss by a violent storm on a rainy night when thunder tore the sky apart. The ancient tree, having lost Ori, attempted to call him back through a light ritual, but the uncontrolled energy backlash plunged it into eternal night, and the once clear cores are now covered with dark patterns. Now, the returning Ori must activate all the eroded cores: when he first touches a core, pure energy will dispel the darkness; however, upon repeated passes, chaotic energy will accumulate to form overload waves. The ancient tree's laws strictly limit that the total number of repeated triggered waves along the entire path must not exceed $k$. At this moment, Ori is suspended in the void woven by the star network. He can start from any core and traverse along the trajectories of the energy branches. Ori needs to plan a path among the winding energy branches to light up the maximum number of cores within the limits. Only by resonating with as many light cores as possible can the true power of the ancient tree be awakened, allowing the healing light to surge again through every leaf vein of Nibel Mountain! Nibel Mountain will welcome dawn, and darkness will eventually be reduced to ashes in the resonance of this star network... Formally, given a non-negative integer $k$, provide an unrooted tree $T=(V,E)$, where $V=\{1,2,\dots,n\}$. Define a path $l=(u_1,u_2,u_3,\dots,u_m)$ composed of $m$ vertices such that for any $1\le i\le m-1$, $(u_i,u_{i+1})\in E$. If there exists $1\le i

The input contains multiple test cases. The first line of data contains an integer $t$ ($1 \leq t \leq 2\times 10^3$) indicating the number of test cases. The following describes each test case. The first line of each test case contains two integers $n$ ($2\le n\le 2\times 10^5$) and $k$ ($0\le k\le n$), separated by a space, representing the number of points on the tree and the maximum number of repeatable points. Note that $k$ can be $0$. The next $n-1$ lines each contain two positive integers $u$ and $v$ ($1\le u,v\le n$), separated by a space, indicating that there is an edge $(u,v)$ on the tree. It is guaranteed that these $n-1$ edges form a tree. It is guaranteed that the sum of $n$ for all test cases does not exceed $2\times 10^5$.

For each test case, output two lines. The first line contains a positive integer $m$, indicating the number of vertices in path $l$. The path $l$ must maximize the size of the essential distinct point set $|V'|$ while satisfying the number of repeated points $s\le k$. The second line contains $m$ positive integers $u_1, u_2, u_3, \dots, u_m$, separated by spaces, indicating that the path $l$ is $(u_1, u_2, u_3, \dots, u_m)$. If there are multiple paths that satisfy the conditions, output any one valid path, and it will be considered correct. It can be proven that for a valid path, $m$ must satisfy $m\le n+k$. The output $m$ must satisfy $m \le n+k$, otherwise it will directly return $\tt{Wrong\ Answer}$.

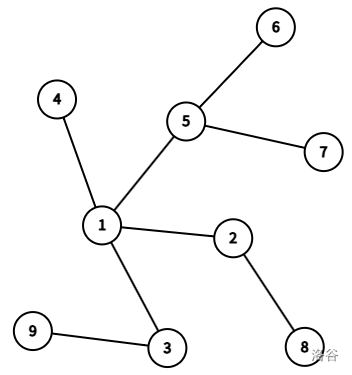
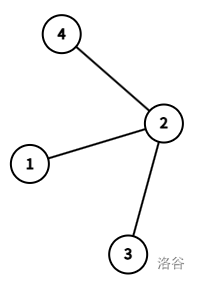
For the first test case, $n=9$ and $k=3$, the tree formed is as follows:  One feasible solution is: $l=(9,3,1,5,7,5,6,5,1,2,8)$. It can be proven that the size of the essential distinct point set $|V'|$ reaches the maximum value of $8$, and the number of repeated points $s=3\le k$. For the second test case, $n=4$ and $k=4$, the tree formed is as follows:  One feasible solution is: $l=(3,2,1,2,4)$. It can be proven that the size of the essential distinct point set $|V'|$ reaches the maximum value of $4$, and the number of repeated points $s=1\le k$. Due to the large input and output data size for this problem, it is recommended to use faster input and output methods.