P12535 [XJTUPC 2025] Bastion

A bastion is the first type of fortress that relies solely on direct firepower and has no attack blind spots.  A simple non-degenerate polygon is a closed polygonal $\textbf{region}$ composed of a sequence of $n$ ($n\ge 3$) vertices, satisfying the following conditions: - The vertex sequence connects end to end, forming $n$ edges, constituting a compact closed set in the plane (including all boundary and interior points); - The $n$ edges only meet at the vertices and do not intersect each other (adjacent edges have no other intersection points outside the common vertex); - The $n$ vertices are distinct, not located inside any non-adjacent edges, and any three consecutive vertices are not collinear. 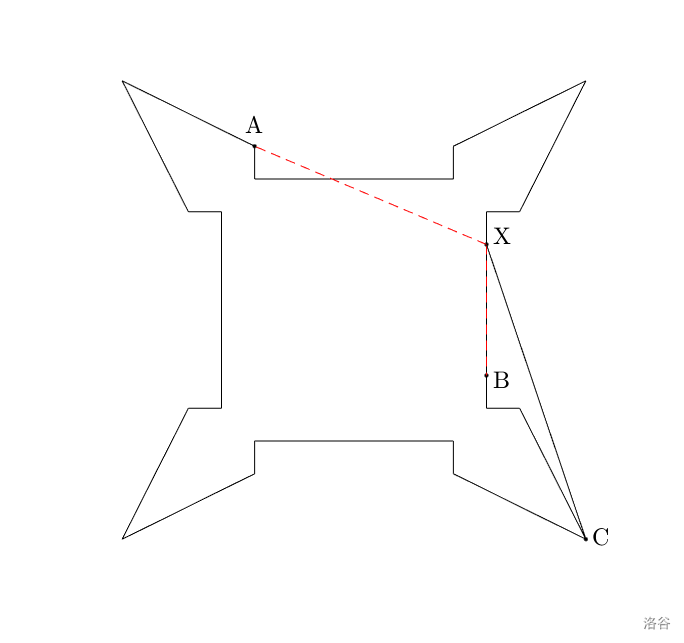The bastion can be viewed as a simple non-degenerate polygon composed of $n$ points and $n$ edges. For two distinct points $P$ and $Q$ on the edges of the polygon, we define that point $P$ can directly fire at point $Q$ if and only if the line segment $PQ$ intersects the polygon only at points $P$ and $Q$. As shown in the figure below, points $A$ and $B$ cannot directly fire at point $X$, but point $C$ can. If there is a point $P$ on the edge of the polygon such that there is no other point $Q$ on the edge of the polygon for which point $Q$ can directly fire at $P$, then we call point $P$ a fire blind spot of the polygon.  We call a simple non-degenerate polygon a bastion if and only if it has at most a finite number of points that are fire blind spots. Given a simple non-degenerate polygon, please determine whether it is a bastion. Formally, given a simple non-degenerate polygon, please determine whether there are only a finite number of points $P$ located on the edges of the polygon such that there is no other point $Q$ on the edges of the polygon for which the line segment $PQ$ intersects the polygon only at points $P$ and $Q$.

The input contains multiple test cases. The first line of the data contains an integer $t$ ($1 \leq t \leq 10^4$) indicating the number of test cases. The following describes each test case. The first line of each test case contains an integer $n$ ($3 \leq n \leq 10^5$), which is the number of edges of the polygon. The next $n$ lines each contain two integers $x_i$ and $y_i$ ($-10^9 \leq x_i, y_i \leq 10^9$), describing a vertex of the polygon. The input data guarantees that a simple non-degenerate polygon is formed. The vertices are given in counterclockwise order, that is, after traversing all the vertices in order, it rotates exactly $360^\circ$ counterclockwise. Connect edges in sequence according to the input order of the vertices (the $i$-th vertex is connected to the $(i+1)$-th vertex, and the $n$-th vertex is connected back to the $1$-st vertex). It is guaranteed that the sum of $n$ for all test cases does not exceed $2 \times 10^5$.

For each test case, output a single line containing a string. If the polygon is a bastion, output $\tt{YES}$; otherwise, output $\tt{NO}$. The answer is case insensitive.