P12548 [UOI 2025] Manhattan Pairing

对于笛卡尔平面上的两个点 $(x_1, y_1)$ 和 $(x_2, y_2)$，我们定义它们之间的*曼哈顿距离*为 $|x_1-x_2|+|y_1-y_2|$。例如，点 $(4, 1)$ 和 $(2, 7)$ 之间的曼哈顿距离为 $|4-2|+|1-7| = 2+6 = 8$。 给定笛卡尔平面上的 $2 \cdot n$ 个点，其坐标均为整数。**所有给定点的 $y$ 坐标要么是 $0$，要么是 $1$。** 将这些点分成 $n$ 对，使得每个点恰好属于一对，并且所有配对中两点之间的最大曼哈顿距离最小化。

第一行包含一个整数 $n$ $(1 \le n \le 10^5)$。 接下来的 $2 \cdot n$ 行，每行包含两个整数 $x_i$ 和 $y_i$ $(0 \le x_i \le 10^9, 0 \le y_i \le 1)$ —— 对应点的坐标。

输出一个整数 —— 最优配对方案中所有配对两点之间的最大曼哈顿距离。

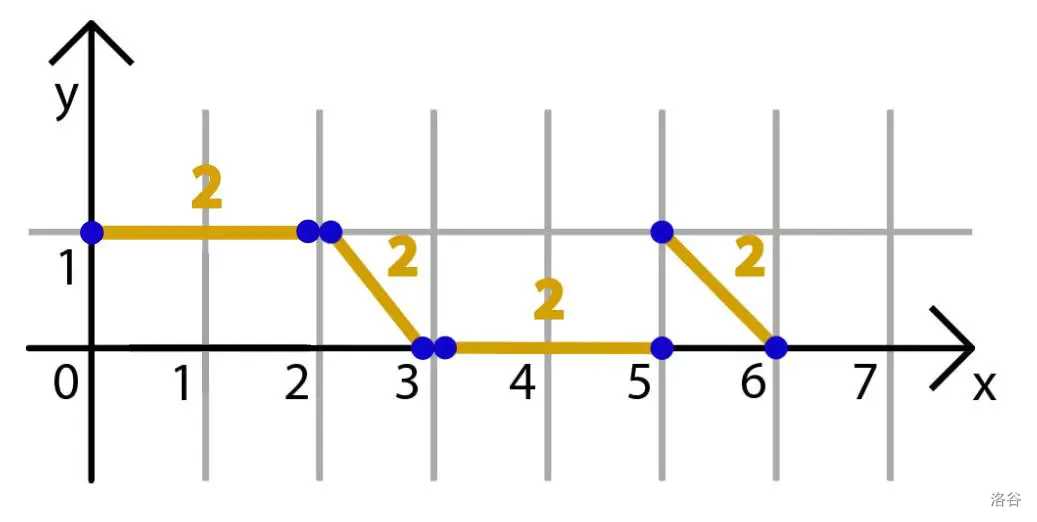
在第二个样例中，配对 $[(18, 0), (14, 0)]$、$[(3, 0), (1, 0)]$ 和 $[(8, 0), (10, 0)]$ 是唯一的最优划分方案。该方案中各对点之间的曼哈顿距离分别为 $4$、$2$ 和 $2$。 在第三个样例中，配对 $[(0, 1), (2, 1)]$、$[(2, 1), (3, 0)]$、$[(3, 0), (5, 0)]$ 和 $[(5, 1), (6, 0)]$ 是一个最优划分方案。该方案中所有配对两点之间的曼哈顿距离均为 $2$。 第三个样例的图示  ### 评分标准 - （$2$ 分）：$n = 1$； - （$3$ 分）：对于所有 $1 \le i \le 2\cdot n$，$x_i = 0$； - （$4$ 分）：$n \le 4$； - （$11$ 分）：$n \le 10$； - （$14$ 分）：对于所有 $1 \le i \le 2\cdot n$，$y_i = 0$； - （$10$ 分）：对于所有 $1 \le i < j \le 2\cdot n$，$x_i \neq x_j$； - （$29$ 分）：$n \le 1000$； - （$27$ 分）：无额外限制。 翻译由 DeepSeek V3 完成