P12553 [UOI 2024] Lady's Gift

在生日那天，女士收到了一份礼物——一个网络。该网络包含 $n$ 个节点，编号为从 $1$ 到 $n$ 的整数。每个节点被分配了一个特定的字母，编号为 $i$ 的节点对应的字母记为 $s_i$。 某些节点对之间存在单向连接。每个节点恰好有一个出向的单向连接。设编号为 $i$ 的节点的连接指向编号为 $x_i$ 的节点。注意 $x_i$ 可以等于 $i$ —— 在这种情况下，认为编号为 $i$ 的节点的连接指向它自身。 定义 $p_{i,0} = i$ 且 $p_{i,k} = p_{x_i,k-1}$。因此，$p_{i,k}$ 表示如果将一枚棋子放在编号为 $i$ 的节点上，并沿着连接移动 $k$ 次后所在的节点编号。 女士构造了一个大小为 $n \times (3 \cdot n)$ 的矩阵 $a$，其中 $a_{i,j} = s_{p_{i,j-1}}$。因此，矩阵 $a$ 的第 $i$ 行是一个长度为 $3 \cdot n$ 的字母序列，其中第一个字母等于 $s_i$，第二个字母等于 $s_{x_i}$，第三个字母等于 $s_{x_{x_i}}$，依此类推。 女士告知了矩阵 $a$ 的某些行，并要求你构造任意一个与已知行相符的网络。

第一行包含一个整数 $n$ $(1 \leq n \leq 2 \cdot 10^3)$ —— 网络中的节点数量。 接下来的 $n$ 行描述矩阵 $a$。每行包含 $3 \cdot n$ 个小写拉丁字母，表示矩阵 $a$ 的对应行；或者仅包含一个符号 ?，表示女士未告知该行。 保证至少存在一个满足条件的网络。

在第一行，输出一个由 $n$ 个小写拉丁字母组成的字符串 $s$ —— 网络中节点上写的字母。 在第二行，输出 $n$ 个整数 $x_1, x_2, \ldots, x_n$ $(1 \leq x_i \leq n)$ —— 各节点的出向连接指向的节点编号。 所构造的网络对应的矩阵必须与女士告知的矩阵 $a$ 在所有已知行上完全一致。 如果存在多个正确答案，输出任意一个即可。

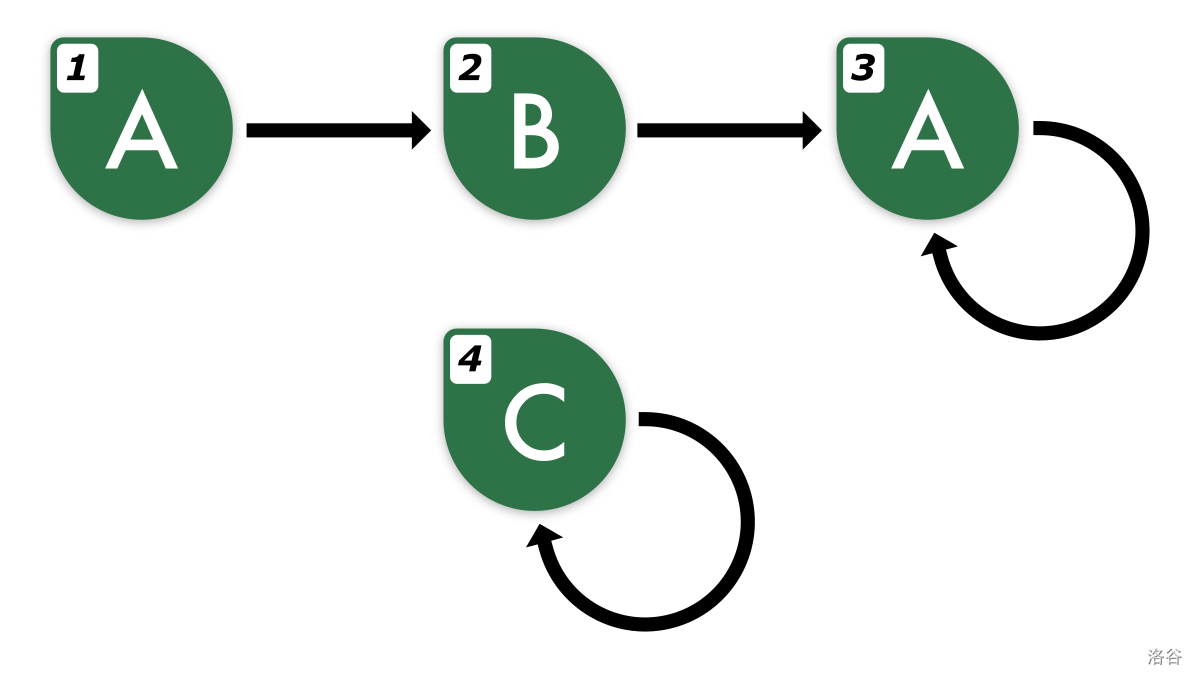
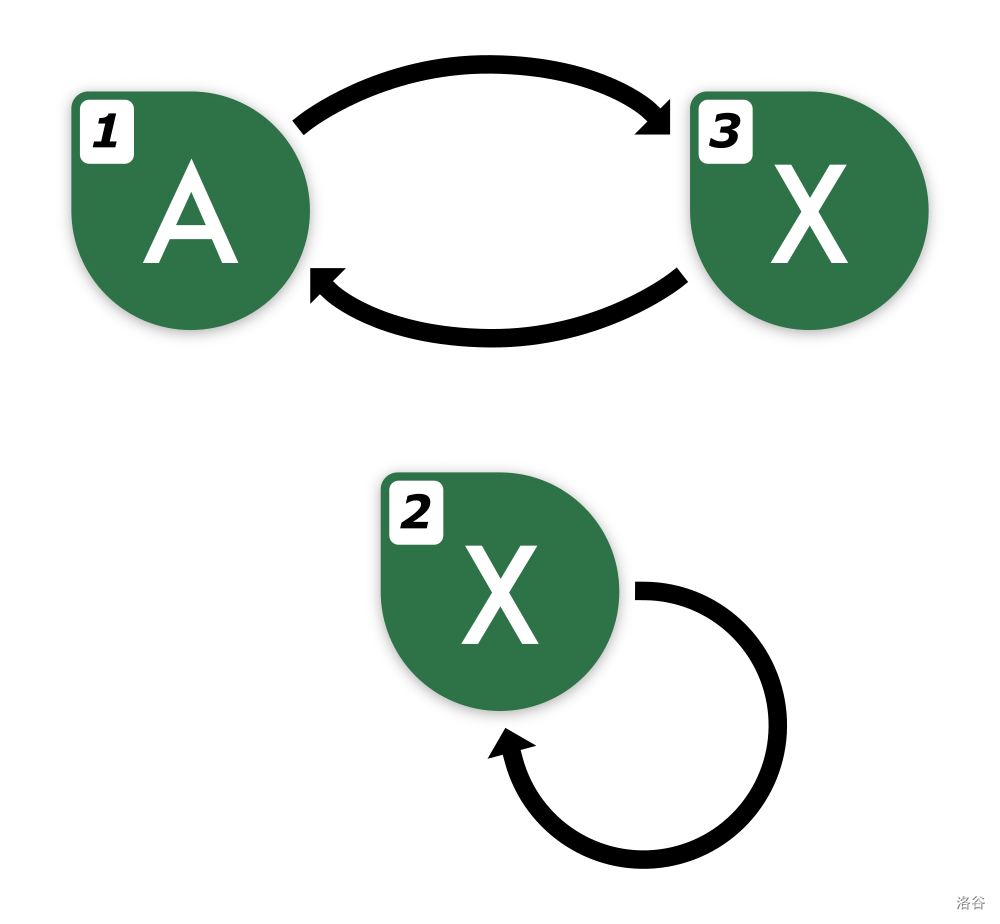
在第一个例子中，$x_1 = 2$ 且 $x_2 = 3$，因此 $p_{1,0}=1$，$p_{1,1}=2$，$p_{1,2}=3$。由于 $x_3=3$，对于所有 $k \geq 3$ 的 $p_{1,k}$ 也等于 $3$。相应地，第一行的第二个字母等于 $s_2$，第三个字母等于 $s_3$。 下方是示例中的网络图示。角落的数字表示节点编号，字母表示对应节点上的字母，箭头表示单向连接。  第一个示例的网络  第二个示例的网络 ### 评分标准 设 $q$ 为女士未告知的行数。 我们称一个网络为"成对节点和孤立节点的集合"，如果该网络可以被划分为：1) 连接指向自身的节点（即 $x_v = v$）；2) 成对的节点 $(a,b)$ 满足 $x_a=b$ 且 $x_b=a$。 我们称一个网络为"星型结构集合"，如果该网络可以被划分为若干个独立的"星型结构"，每个星型结构包含：1) 一个主节点 $v$（满足 $x_v = v$）；2) 一组从节点 $y=\{y_1, y_2, \ldots, y_k\}$（满足 $x_{y_i}=v$ 对 $1 \leq i \leq k$ 成立）。注意网络中的星型结构可以有不同的尺寸，甚至可以仅包含一个主节点。 我们称一个网络为"以节点 $v$ 为根的树形结构"，如果：1) 节点 $v$ 的连接指向自身（即 $x_v = v$）；2) 其他所有节点都能通过网络连接到达节点 $v$（即对每个 $1 \leq i \leq n$ 都存在 $k$ 使得 $p_{i,k}=v$）。 我们称一个网络为"环形结构"，如果从任意节点出发都能通过网络连接到达其他所有节点（即对所有 $1 \leq i,j \leq n$ 都存在 $k$ 使得 $p_{i,k}=j$）。 评分细则如下： - （10 分）：$n \leq 5$，$q = 0$； - （6 分）：$n \leq 300$，$q = 0$，且对所有 $1\le i\le n$ 有 $x_{x_i}=i$（网络是成对节点和孤立节点的集合）； - （6 分）：$n \leq 300$，$q = 0$，且对所有 $1\le i\le n$ 有 $x_{x_i}=x_i$（网络是星型结构集合）； - （9 分）：$n \leq 300$，$q = 0$，且 $x_1=1$，对所有 $2\le i \le n$ 有 $x_i