P12557 [UOI 2024] Football

There are $n$ players in a football team, numbered with integers from $1$ to $n$. The skill level of player with number $i$ is described by the integer $c_i$. The players are arranged in a circle in such a way that the player with number $i$ has the player with number $i+1$ on their right side (for $1 \le i < n$), and for the player with number $n$, the next player is the one with number $1$. Let's define the **strength** of a game combination, characterized by an array of integers $k=[k_0, k_1, k_2, \ldots, k_{m-1}]$, as follows: - initially, the ball is with the player with number $1$; - the players pass the ball in turns indefinitely: when performing the pass with number $i$, the player who currently has control of the ball passes it to the player located $x$ positions to the right in the circle, where $x=k_{((i-1) \mod m)}$; - the **strength** of the game combination is considered to be the minimum skill level among the skills of all players who had the ball at some point during the described process. An array of integers $a_0,a_1,\ldots,a_{q-1}$ is given. For each $i$ from $0$ to $(q-1)$, find the strength of the game combination characterized by the array $[a_0,a_1,\ldots,a_i]$.

The first line contains two integers $n$ and $q$ $(1 \leq n, q \leq 3\cdot{10}^5)$ --- the number of players and the length of the array $a$. The second line contains $n$ integers $c_1, c_2, \dots, c_n$ $(1 \leq c_i \leq n)$ --- the skill levels of the players. The third line contains $q$ integers $a_0, a_1, \dots, a_{q-1}$ $(1 \leq a_i \leq n-1)$ --- the elements of the array $a$.

Output $q$ integers --- the sought values of the strengths of game combinations.

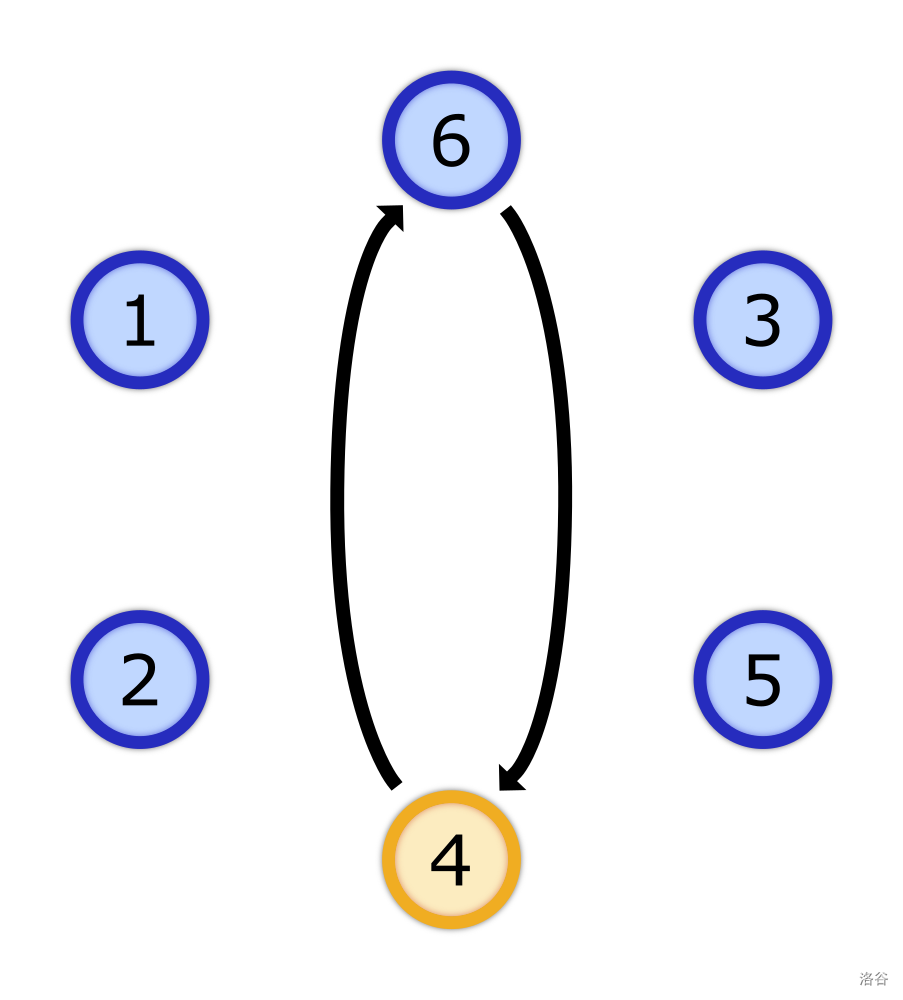
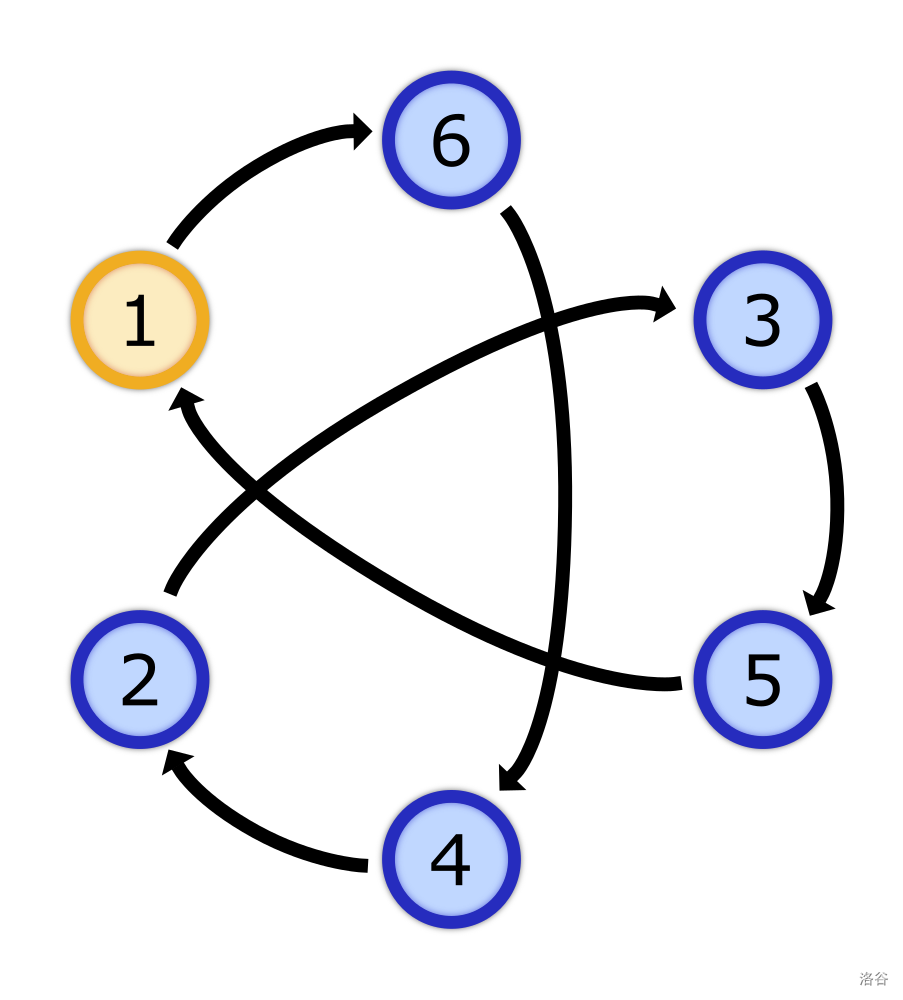
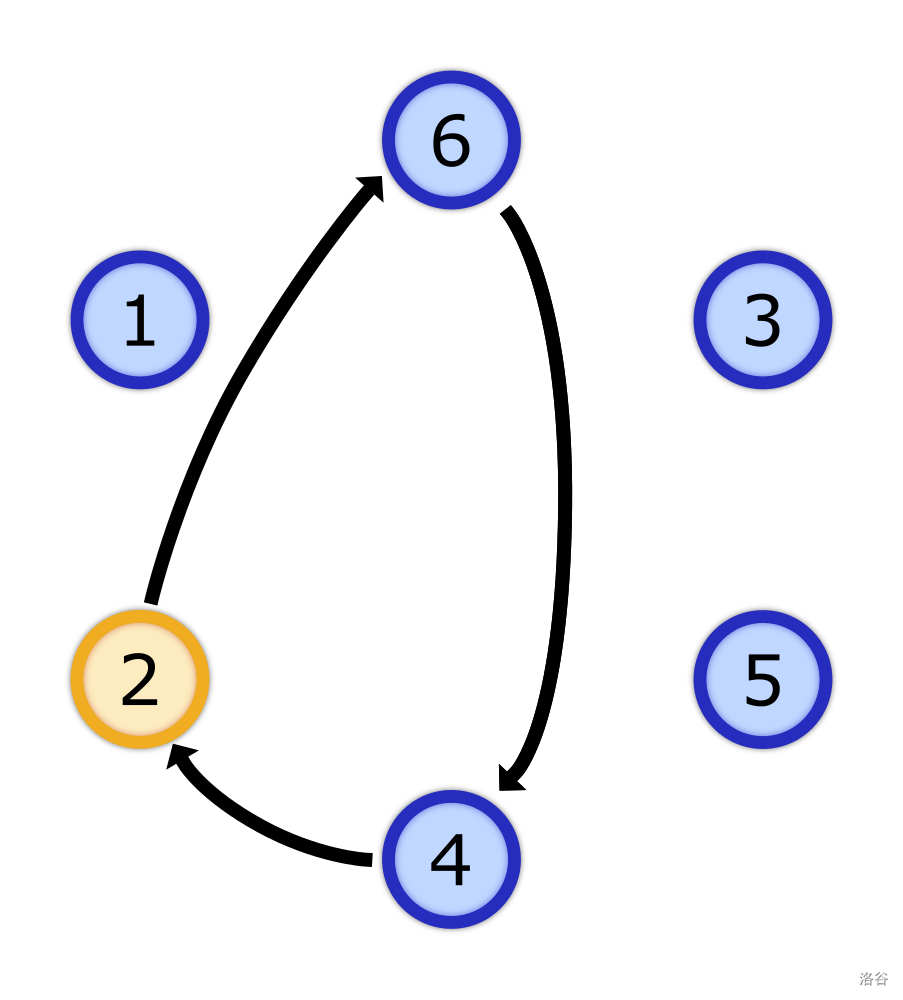
In the example of passing the ball for game combinations, it looks as follows:  $k=[3]$  $k=[3,1]$  $k=[3,1,2]$ ### Scoring - ($10$ points): $n, q \leq 100$; - ($4$ points): all values of $a_i$ are the same; - ($11$ points): $n$ is a prime number; - ($12$ points): $n, q \leq 1000$; - ($16$ points): $n, q \leq 1.5\cdot{10}^5$, $n = 2^k$ for some integer $k$; - ($25$ points): $n, q \leq {10}^5$; - ($22$ points): without additional constraints.