P12558 [UOI 2024] Heroes and Monsters

有 $n$ 个英雄和 $n$ 个怪物。英雄和怪物分别编号为 $1$ 到 $n$ 的整数。第 $i$ 个英雄的战斗力为 $a_i$，第 $i$ 个怪物的战斗力为 $b_i$。保证所有 $a_1, a_2, \ldots, a_n, b_1, b_2, \ldots, b_n$ 的值都是**两两不同**的。 将进行总共 $n$ 场战斗。每场战斗中恰好有一个英雄和一个怪物参与，且每个英雄和每个怪物都恰好参与一场战斗。假设某场战斗由编号为 $i$ 的英雄和编号为 $j$ 的怪物进行。如果 $a_i > b_j$，则编号为 $i$ 的英雄会感到高兴；否则，他会感到悲伤。 定义 $ans_k$ 为大小为 $k$ 的不同英雄集合 $S$ 的数量，满足存在一种战斗分配方式使得集合 $S$ 中的所有英雄都高兴，而其他英雄都悲伤。 给定 $q$ 个形如 $l$、$r$ 的查询。对于每个查询，计算 $(\sum\limits_{i=l}^{r} ans_i) \mod 998244353$ 的值。

第一行包含一个整数 $n$（$1 \leq n \leq 5 \cdot 10^3$）—— 将进行的战斗场数。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \leq a_i \leq 2 \cdot n$）—— 英雄的战斗力。 第三行包含 $n$ 个整数 $b_1, b_2, \ldots, b_n$（$1 \leq b_i \leq 2 \cdot n$）—— 怪物的战斗力。 保证所有 $a_1, a_2, \ldots, a_n, b_1, b_2, \ldots, b_n$ 的值都是两两不同的。 第四行包含一个整数 $q$（$1 \leq q \leq n+1$）—— 查询的数量。 接下来的 $q$ 行每行包含两个整数 $l$ 和 $r$（$0 \leq l \leq r \leq n$）—— 对应查询的参数。 保证所有 $a_1, a_2, \ldots, a_n, b_1, b_2, \ldots, b_n$ 的值都是两两不同的。

对于每个查询，输出一个整数 —— 所求的值 $(\sum\limits_{i=l}^{r} ans_i) \mod 998244353$。

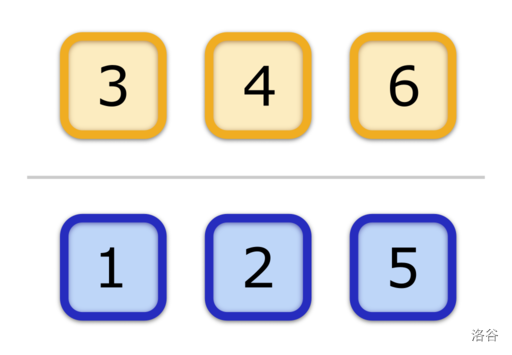
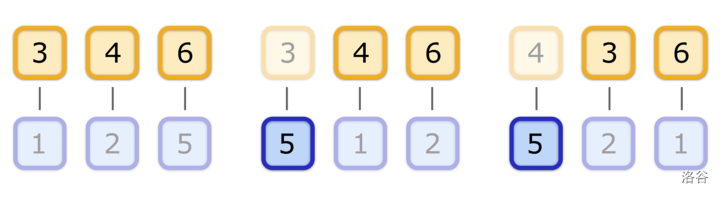
下图展示了第一个样例中的英雄和怪物。英雄位于上方，怪物位于下方。方块中的数字表示对应英雄或怪物的战斗力。  在样例中，存在三个可能的高兴英雄集合：$\{1,2,3\}$、$\{2,3\}$ 和 $\{1,3\}$。以下是三种可能的战斗分配方式，使得对应的英雄集合高兴。注意，可能存在多种战斗分配方式使得同一个英雄集合高兴。  ### 评分标准 - （$3$ 分）：对于所有 $1 \leq i,j \leq n$，满足 $a_i < b_j$； - （$9$ 分）：$q = 1$，$l = 1$，$r = 1$； - （$6$ 分）：对于所有 $1 \leq i \leq n$，满足 $a_i = 2 \cdot i - 1$，$b_i = 2 \cdot i$； - （$16$ 分）：$n \leq 500$，$q = 1$，$l = 0$，$r = n$； - （$14$ 分）：$q = 1$，$l = 0$，$r = n$； - （$15$ 分）：$q = 1$，$l = r$； - （$17$ 分）：$n \leq 500$； - （$20$ 分）：无额外限制。 翻译由 DeepSeek V3 完成