P12558 [UOI 2024] Heroes and Monsters

There are $n$ heroes and $n$ monsters. The heroes and monsters are numbered with integers from $1$ to $n$. The strength of the $i$-th hero is equal to $a_i$, and the strength of the $i$-th monster is equal to $b_i$. It is guaranteed that all values $a_1, a_2, \ldots, a_n, b_1, b_2, \ldots, b_n$ are **pairwise distinct**. There will be a total of $n$ battles. In each battle, exactly one hero and exactly one monster will participate, with each hero and each monster participating in exactly one battle. Let the battle involve the hero with number $i$ and the monster with number $j$. If $a_i>b_j$, then the hero with number $i$ will be happy, otherwise, he will be sad. Let $ans_k$ be the number of different sets of heroes $S$ of size $k$, such that there is a distribution of battles where all heroes in $S$ will be happy and all other heroes will be sad. Given $q$ queries of the form $l$, $r$. For each query, find $(\sum\limits_{i=l}^{r} ans_i) \mod 998244353$.

The first line contains a single integer $n$ ($1 \leq n \leq 5 \cdot 10^3$) --- the number of battles that will take place. The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($1 \leq a_i \leq 2 \cdot n$) --- the strengths of the heroes. The third line contains $n$ integers $b_1, b_2, \ldots, b_n$ $(1 \leq b_i \leq 2 \cdot n)$ --- the strengths of the monsters. It is guaranteed that all values $a_1, a_2, \ldots, a_n, b_1, b_2, \ldots, b_n$ are pairwise distinct. The fourth line contains a single integer $q$ $(1 \leq q \leq n+1)$ --- the number of queries. The next $q$ lines contain two integers each, $l$ and $r$ $(0 \leq l \leq r \leq n)$ --- the parameters of the corresponding query. It is guaranteed that all values $a_1, a_2, \ldots, a_n, b_1, b_2, \ldots, b_n$ are pairwise distinct.

For each query, output a single integer --- the required value $(\sum\limits_{i=l}^{r} ans_i) \mod 998244353$.

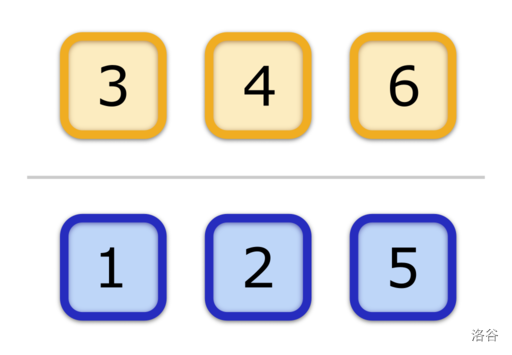
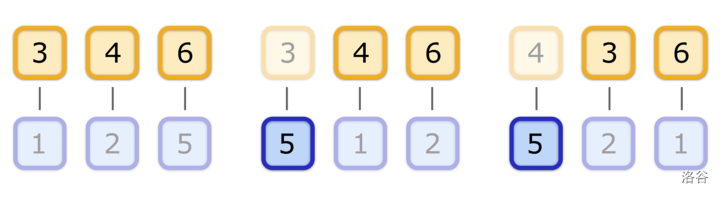
The image below shows the heroes and monsters of the first example. The heroes are at the top, and the monsters are at the bottom. The number inside the square represents the strength of the corresponding hero or monster.  In the example, there are three possible sets of happy heroes: $\{1,2,3\}$, $\{2,3\}$, and $\{1,3\}$. Below are three possible distributions of battles in which the corresponding sets of heroes will be happy. Note that there may be multiple distributions of battles where the same set of heroes will be happy.  ### Scoring - ($3$ points): $a_i < b_j$ for $1 \leq i,j \leq n$; - ($9$ points): $q = 1$, $l = 1$, $r = 1$; - ($6$ points): $a_i = 2 \cdot i - 1$, $b_i = 2 \cdot i$ for $1 \leq i \leq n$; - ($16$ points): $n \leq 500$, $q = 1$, $l = 0$, $r = n$; - ($14$ points): $q = 1$, $l = 0$, $r = n$; - ($15$ points): $q = 1$, $l=r$; - ($17$ points): $n \leq 500$; - ($20$ points): without additional restrictions.