P1256 Displaying the Image

An old display screen consists of $N \times M$ pixels. The position of a pixel is determined by its row and column. For example, $P(2,1)$ denotes the pixel at row $2$, column $1$. At that time, the screen could only show two colors, black and white, represented by binary $0$ and $1$. $0$ denotes black and $1$ denotes white. When the computer issues an instruction $P(x,y)=1$, the cathode ray tube at row $x$, column $y$ on the screen starts working, making that pixel display white; if $P(x,y)=0$, then the corresponding cathode ray tube does not work, and the pixel remains black. At a certain moment, the computer issues a command for the entire screen in the form of an $N \times M$ two-dimensional $01$ matrix. For example, the screen consists of $3 \times 4$ pixels. 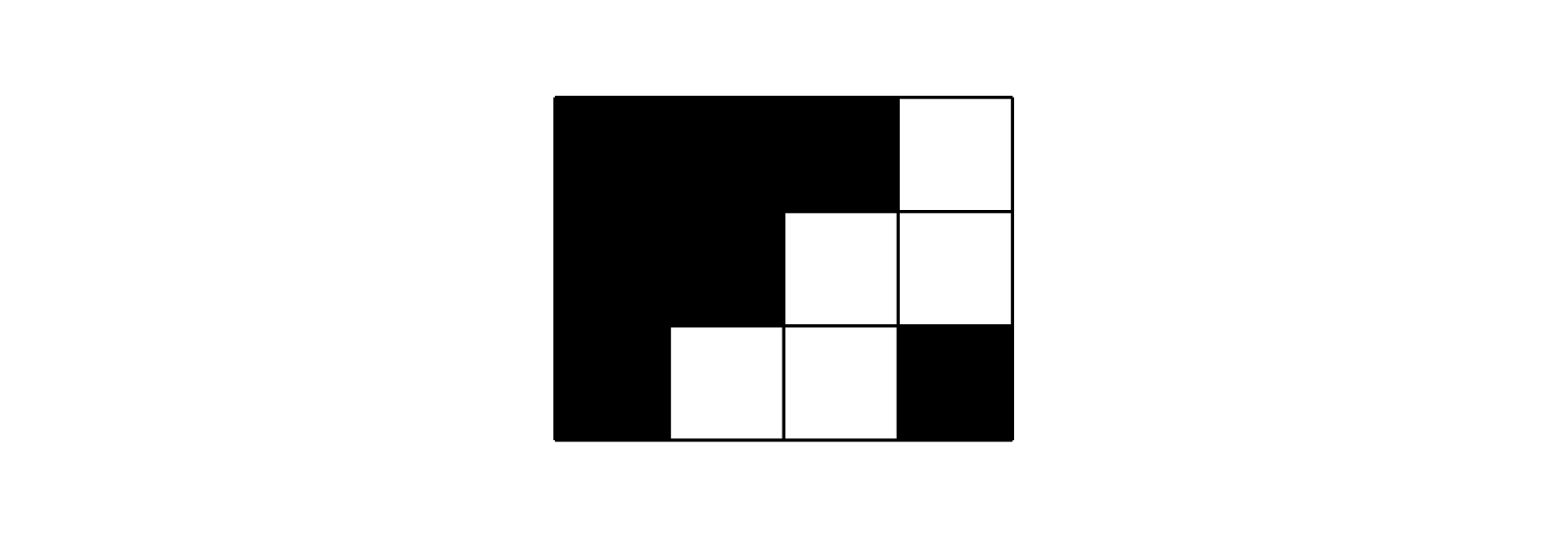At some moment, the computer issues the following command: $$\begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ \end{pmatrix}$$ The corresponding screen display should be:  Assume that after magnification, one cell represents one pixel. For unknown reasons, black pixels are always affected by white pixels—possibly due to the operation of the cathode ray tube. Moreover, the closer the distance, the greater the influence. The distance is defined as follows: Given pixel $P_1(x_1,y_1)$ and pixel $P_2(x_2,y_2)$, their distance is $D(P_1,P_2)=|x_1-x_2|+|y_1-y_2|$. At a certain moment after the display command is issued, scientists want to know, for each pixel, the shortest distance to its nearest white pixel—scientists guarantee that there is at least one white pixel on the screen. In the example above, the distance between pixel $P(1,1)$ and its nearest white pixel is $3$, while pixel $P(3,2)$ itself is white, so the shortest distance is $0$.

The first line contains two numbers, $N$ and $M\ (1 \le N,M \le 182)$, indicating the screen size. The next $N$ lines each contain $M$ numbers, $0$ or $1$. This is the display command issued by the computer.

Output $N$ lines, each containing $M$ numbers separated by a single space. The number in row $i$, column $j$ indicates the shortest distance from pixel $P(i,j)$ to its nearest white pixel.

- For $30\%$ of the testdata: $N\times M \le 10000$. - For $100\%$ of the testdata: $N\times M \le 182^2$. Translated by ChatGPT 5