P12576 [UOI 2021] 数字图
题目描述
瓦西里和彼得里克发现了一个数字图——这是一个连通的有向图,每个顶点上都标有一个数字。
两人急需一个数字,于是决定在图上游玩一个游戏。他们将棋子放在编号为 1 的顶点上。每一回合可以选择以下两种操作之一:
1. 结束游戏并获得当前顶点上的数字;
2. 沿着有向边将棋子移动到相邻顶点。
如果游戏进行到 $10^{100}$ 回合仍未结束,则自动终止并获得当前顶点上的数字。
瓦西里先手,他希望最大化最终获得的数字;而彼得里克则希望最小化这个数字。假设双方都采取最优策略,求游戏结束时他们将获得的数字。
输入格式
第一行包含两个整数 $n$ 和 $m$($1 \leq n \leq 250\,000$,$1 \leq m \leq 500\,000$)——分别表示图的顶点数和边数。
第二行包含 $n$ 个整数 $a_i$($1 \leq a_i \leq 10^9$)——表示每个顶点上的数字。
接下来的 $m$ 行,每行包含两个整数 $x$ 和 $y$($1 \leq x, y \leq n$),表示存在一条从顶点 $x$ 指向 $y$ 的有向边。
输出格式
输出一个整数,表示在双方都采取最优策略时,游戏结束时获得的数字。
说明/提示
第一个样例的图示如图 1 所示,顶点标注格式为"顶点编号(数字)":
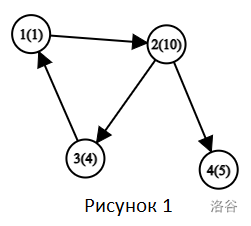
1. 瓦西里先手,可以选择立即结束游戏或移动到顶点 2。最优选择是移动。
2. 彼得里克回合,最优选择是移动到顶点 3。
3. 最后如果瓦西里移动到顶点 1,彼得里克会结束游戏获得数字 1,因此瓦西里会选择直接结束游戏获得数字 4。
第二个样例的图示如图 2 所示:
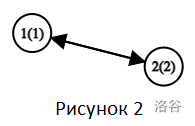
双方将交替移动 $10^{100}$ 步,最终棋子停留在顶点 1。
### 评分标准
1. ($6$ 分)给定的图是一条所有边同向的直线;
2. ($8$ 分)给定的图是一棵以顶点 1 为根的树,所有边方向从根向下;
3. ($14$ 分)给定的图是一个环;
4. ($26$ 分)$1 \leq a_i \leq 2$;
5. ($46$ 分)无额外限制。
翻译由 DeepSeek V3 完成