P12583 「KTSC 2019 R1」山羊【暂时无法评测】

**本题因官方交互库在洛谷出现编译错误暂时无法评测，目前正在尝试修复。** **请使用 C++17 或 C++20 提交本题** 你需要在程序开头加入如下代码： ```cpp #include void init(std::vector X, std::vector Y); int count(int A, int B, int C); ``` 题目译自 [2019년도 국제정보올림피아드 대표학생 선발고사 - 1차 선발고사](https://www.ioikorea.kr/archives/ioitst/2019/) T2「[트리](https://assets.ioikorea.or.kr/ioitst/2019/1/goat/goat_statement.pdf)」

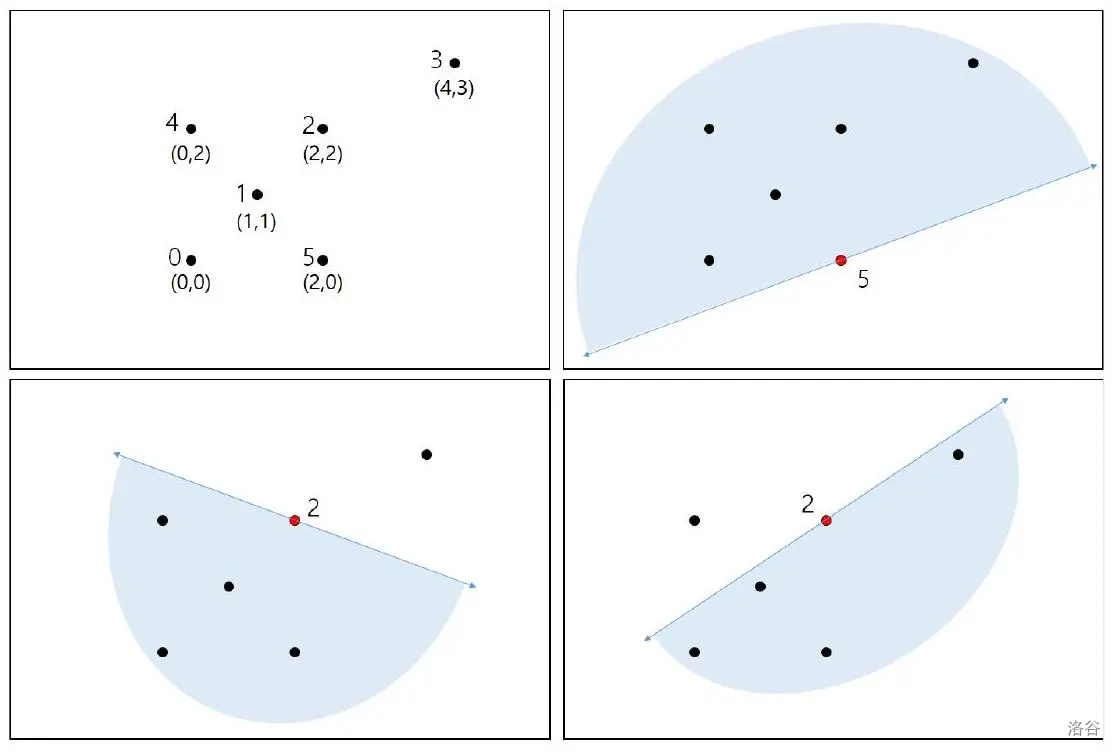
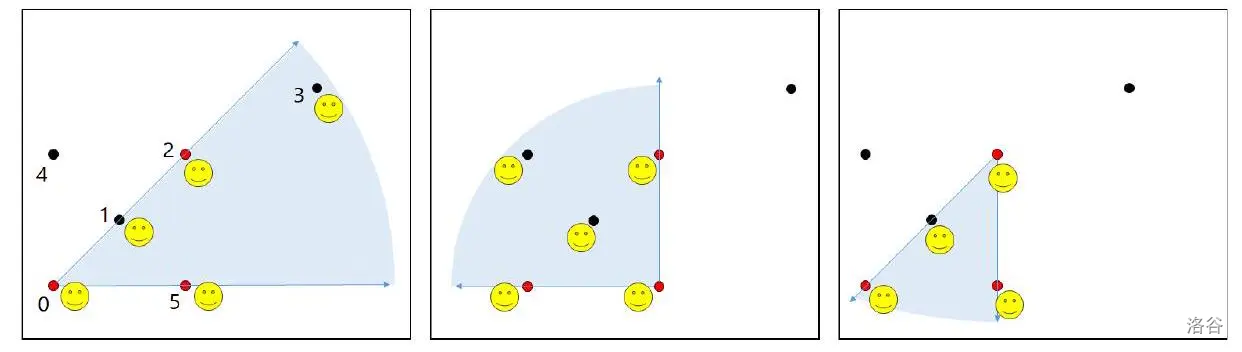
在广阔的平原上有 $N$ 头山羊。没有两个或以上的山羊在同一位置。这些山羊都是机器人，只能在原地旋转。山羊的鼻子上有 LED 灯，可以远程点亮。山羊的眼睛是可以实时远程查看摄像头捕获的图像，并可以保存想要的场景。山羊可以看到自己，也有透视功能，即使山羊重叠也能知道有多少只。山羊的左右视野为 $180^{\circ}$，在 $180^{\circ}$ 边界上的物体也能看见。 根据山羊的位置，有些山羊可以一次看到 $N$ 头山羊，而有些山羊无论朝哪个方向看都无法一次看到 $N$ 头山羊。例如，下面的图中，编号为 $0$ 到 $5$ 的六只山羊中，$5$ 号山羊可以一次看到六只山羊，但 $2$ 号山羊无论朝哪个方向看都无法一次看到六只山羊。  为了进行特殊的实验，我们选择两只一次能看到 N 头山羊的不同山羊，再从剩下的山羊中任意选择一只。这三只选定的山羊将点亮鼻子，以便随时确认它们的位置。观察选定三只山羊眼中捕获到的图像，并在每只山羊能看到点亮的三只山羊同框的场景下各自保存一张图像。然后，逐一查看保存的三张图像，对每张图像中点亮的两只其他山羊之间（包括边界）可见的所有山羊进行特殊标记。这个标记是为了特殊的实验，实验的目标是统计 $N$ 只山羊中被标记了三次的山羊数量。 例如，如果在全部六只山羊中选定的三只山羊用红点表示，下面的图显示了以每只山羊为基准被特殊标记的山羊。（当然，每张图并非是保存的场景本身。）在这种情况下，被标记了三次的山羊数量是 $4$。  你需要为这个实验实现以下两个函数： - `void init(int x[], int y[]);` 最先被调用，并且只调用一次。`x` 和 `y` 是大小为 $N$ 的数组（向量）。`x[0..N-1]` 表示山羊的 $x$ 坐标，`y[0..N-1]` 表示山羊的 $y$ 坐标。编号为 $i (0 \leq i \leq N-1)$ 的山羊位置是 `(x[i], y[i])`。 - `int count(int a, int b, int c);` 使用给定的三只山羊的坐标 `(x[a], y[a])`，`(x[b], y[b])`，`(x[c], y[c])`，计算被标记了三次的山羊数量并返回。

示例评测程序以以下格式读取输入： - 第 $1$ 行：$N\, Q$，其中 $N$ 表示山羊的数量，$Q$ 表示查询的数量 - 接下来的 $N$ 行：每行两个整数 $x\, y$，表示山羊位置的 $x$ 坐标和 $y$ 坐标 - 接下来的 $Q$ 行：每行三个整数 $a\,b\,c (0 \leq a, b, c \leq N-1)$，表示三只山羊的编号

示例评测程序对每个查询输出一行一个整数，表示满足条件的山羊数量。

### 样例说明 #1 下面是样例 1 的函数调用及其结果： | 函数调用 | 返回值 | | :-----------: | :-----------: | |`init({0, 1, 2, 4, 0, 2}, {0, 1, 2, 3, 2, 0})`| | |`count(0, 5, 2)`|$4$| |`count(1, 3, 4)`|$4$| |`count(4, 1, 5)`|$3$| ### 数据范围 对于所有输入数据，满足： - $3 \leq N \leq 3\,000$ - $1 \leq Q \leq 5 \times 10^{6}$ - 所有山羊的 $x$ 坐标和 $y$ 坐标都在 $0$ 到 $10^{9}$ 之间 详细子任务附加限制及分值如下表所示。 | Subtask | 分值 | 约束 | | :----------: | :----------: | :----------: | | $1$ | $5$ | $N \leq 500, Q \leq 10^{5}$；任何三点不在一条直线上 | | $2$ | $17$ | $N \leq 500, Q \leq 10^{5}$ | | $3$ | $10$ | $N \leq 500$；任何三点不在一条直线上 | | $4$ | $8$ | $N \leq 500$ | | $5$ | $29$ | 任何三点不在一条直线上 | | $6$ | $31$ | 无附加限制 |