P12586 「KTSC 2019 R2」嫩芽

**请使用 C++17 或 C++20 提交本题** 你需要在程序开头加入如下代码： ```cpp #include int diff(int K, std::vector V); ``` 题目译自 [2019년도 국제정보올림피아드 대표학생 선발고사 - 2차 선발고사](https://www.ioikorea.kr/archives/ioitst/2019/) T1「[새싹](https://assets.ioikorea.kr/ioitst/2019/1/sprout/sprout_statement.pdf)」

巴库将一块大的正方形地均匀分割成了 $N \times N$ 个小方形田地。在每块田地里撒下了 $P$ 颗种子，一周后，有些种子发了芽，有些还没有发芽。比如，下面的图显示了 $6 \times 6$ 田地中每块田地发芽的情况。最左上角的田地里有两颗芽，而最右下角的田地里只有一颗芽。  观察田地时，巴库想到了最近学到的中位数。中位数是奇数个给定值中的一个，当这些值排序时，正好位于中间的那个值。比如，五个给定值是 $0,1,2,2,3$ 时，中位数是 $2$。 巴库想知道中位数和平均数之间的差异有多大，所以他决定比较每块田地发芽数量的中位数和平均数。为了进行多种情况的比较，他决定在相邻的 $K \times K$ 个田地上计算中位数和平均数。这样的话，可以在给定的 $N \times N$ 田地上总共进行 $(N-K+1) \times(N-K+1)$ 次比较。 例如，对于上图中的田地，用 $3 \times 3$ 的区域计算中位数和平均数结果如下表。最左上角的 $3 \times 3$ 田地中发芽数量是 $2, 1, 0, 0, 1, 0, 2, 0, 1$，因此中位数是 $1$，平均数是 $\frac{7}{9}$。最右上角的 $3 \times 3$ 田地中，中位数是 $0$，平均数是 $\frac{8}{9}$。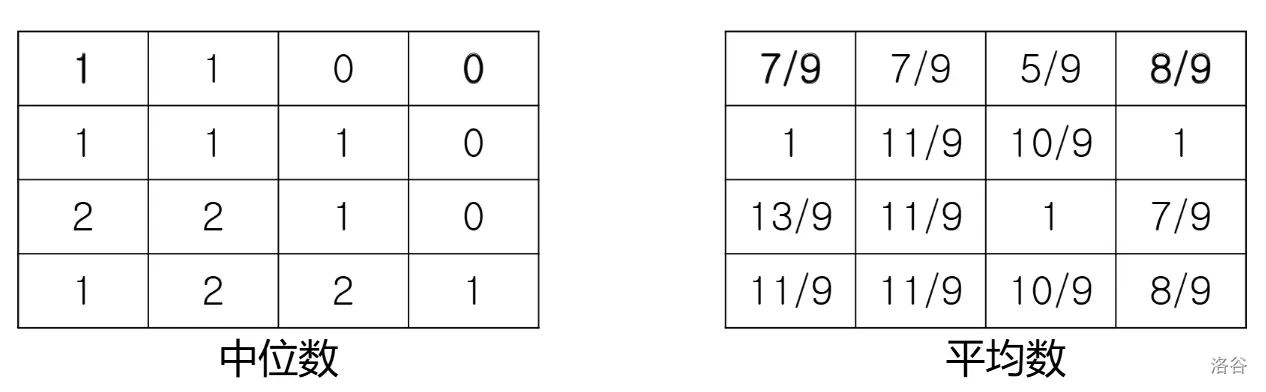  巴库想知道中位数和平均数差值的最大值。在上例中，最大差值出现在下图中标红色边框的部分，中位数是 $0$，平均数是 $1$，两者差值是 $1$。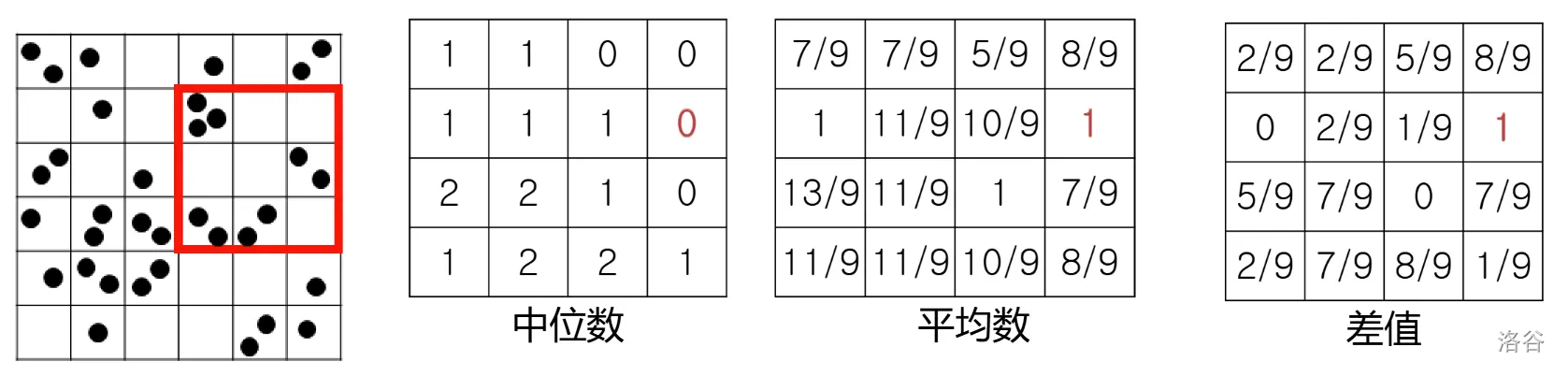  巴库为了方便计算，决定找出中位数和平均数差值乘以 $K^{2}$ 后的最大值。所以，在上例中最大值是 $9$。你需要为巴库实现以下函数： `int diff(int K, int V[][]);` 该函数只会被调用一次，`V` 是大小为 $N \times N$ 的数组（向量），每块田地发芽的数量 `V[0..N-1][0..N-1]` 是传入的参数。函数需要计算出 $K \times K$ 区域中中位数和平均数的差值乘以 $K^{2}$ 的最大值并返回。 这些函数必须按照上述描述工作。当然，你可以创建和使用其他函数，但不得进行任何输入输出操作或访问其他文件。

示例评测程序按以下格式读取输入： - 第 $1$ 行：$N\,K$，其中 $N$ 表示田地的大小，$K$ 表示区域的大小。 - 接下来的 $N$ 行：$V_{i,0}\, V_{i,1}\,\cdots \,V_{i,N-1}$，其中 $V_{i,0}\, V_{i,1}\, \cdots\, V_{i,N-1}$ 表示第 $i$ 行的发芽数量。

示例评测程序会输出你在 `diff()` 函数中返回的值。

对于所有输入数据，满足： - $1 \leq N \leq 2000$ - $K$ 为奇数，$1 \leq K \leq N$ - $0 \leq V_{i,j} \leq 30 (0 \leq i, j \leq N-1)$ 详细子任务附加限制及分值如下表所示。 | 子任务 | 分值 | 附加限制 | | :----------: | :----------: | :----------: | |$1$|$17$|$N \leq 100$| |$2$|$24$|$N \leq 300$| |$3$|$42$|$N \leq 700$| |$4$|$67$|无附加限制|