P12589 「KTSC 2019 R2」大平原

**请使用 C++17 或 C++20 提交本题** 你需要在程序开头加入如下代码： ```cpp #include #include #include using namespace std; long long shortest_path(pair src, pair dst, vector p1, vector p2, vector w); ``` 题目译自 [2019년도 국제정보올림피아드 대표학생 선발고사 - 2차 선발고사](https://www.ioikorea.kr/archives/ioitst/2019/) T4「[다각형](https://assets.ioikorea.kr/ioitst/2019/1/plain/plain_statement.pdf)」

一只蚂蚁在大平原上从起点移动到终点，它以每公里 $100$ 分钟的速度前进。蚂蚁只能平行于 $x$ 轴和 $y$ 轴移动，在丘陵地带移动时间可能会增加。给定起点、终点、丘陵地带的范围和每个丘陵地带 $1$ 公里的移动时间，计算蚂蚁从起点到终点所需的最短时间。 丘陵地带是由平行于 $x$ 轴和 $y$ 轴的边组成的矩形，每个矩形都有 $1$ 公里的移动时间。这段时间只适用于矩形的内部，不适用于边界。此外，不同的矩形不会重叠，起点、终点和不同的矩形的顶点坐标都是整数且不重叠。起点和终点始终位于所有矩形的外部。 例如，下图显示了两个矩形，其中一个矩形的左下角坐标为 $(0,1)$，右上角坐标为 $(5,2)$，每公里移动时间为 $200$ 分钟。另一个矩形的左下角坐标为 $(4,3)$，右上角坐标为 $(9,4)$，每公里移动时间为 $1000$ 分钟。图中标注了从点 $A$ 到点 $B$ 以及从点 $C$ 到点 $D$ 的最短时间路径，它们分别为 $700$ 分钟和 $1000$ 分钟。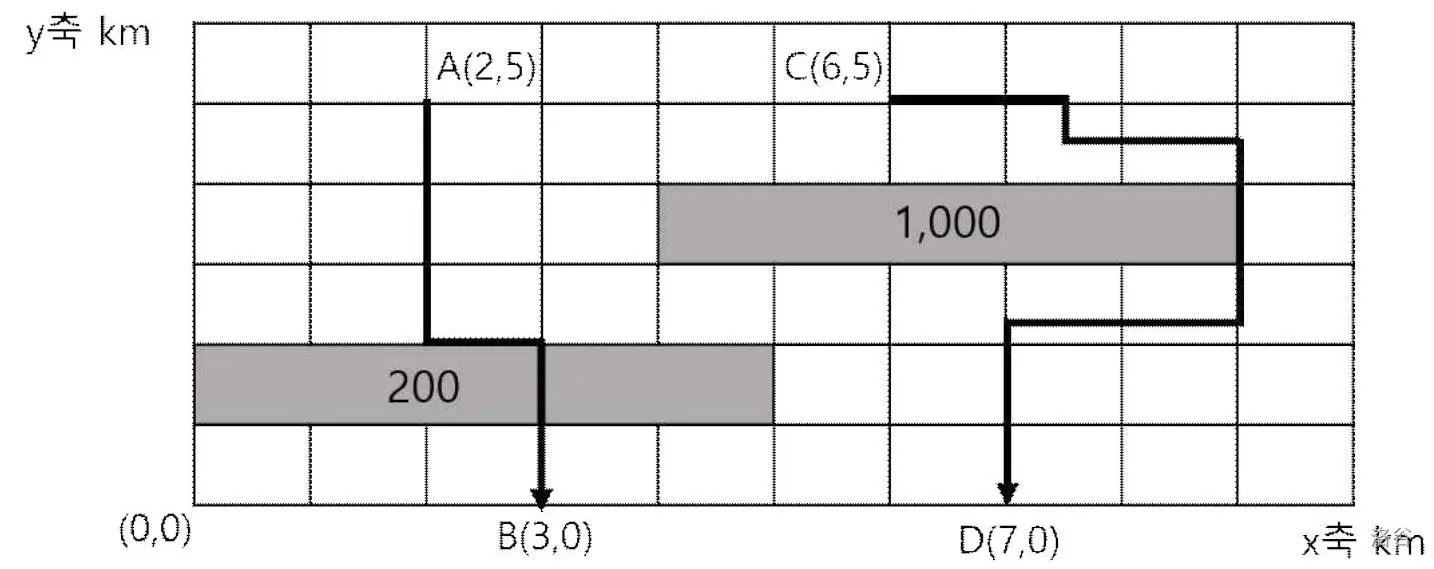  你需要实现以下函数： - `long long shortest_path(pair src, pair dst, vector p1, vector p2, vector w);` 这个函数只会调用一次。`src` 和 `dst` 分别是起点和终点。每个矩形的左下角坐标在 `p1`，右上角坐标在 `p2`。利用给定的值计算从 `src` 到 `dst` 的最短时间并返回。 函数必须按照上述描述进行操作。当然，你可以创建和使用其他函数，但不得进行任何输入输出操作或访问其他文件。

示例评测程序按以下格式读取输入。$x, y$ 坐标的单位为公里： - 第 $1$ 行：$N\,x_{s}\,y_{s}\,x_{e}\,y_{e}$，其中 $N$ 表示矩形的数量，$x_{s}, y_{s}$ 表示起点的 $x$ 和 $y$ 坐标，$x_{e}, y_{e}$ 表示终点的 $x$ 和 $y$ 坐标 - 接下来的 $N$ 行：每行给出一个矩形的坐标和移动时间 $x_{1}\,y_{1}\,x_{2}\,y_{2}\,w$，其中 $x_{1}, y_{1}$ 表示矩形左下角的 $x$ 和 $y$ 坐标，$x_{2},y_{2}$ 表示矩形右上角的 $x$ 和 $y$ 坐标，$w$ 表示矩形内部的 $1$ 公里移动时间

示例评测程序会输出 `shortest_path` 函数的返回值。

对于所有输入数据，满足： - $1 \leq N \leq 10^5$ - $100 \leq w \leq 10^{8}$ - $0 \leq x, y \leq 10^{8}$（$x, y$ 是起点、终点或矩形的顶点坐标） - $N, w, x, y$ 都是整数 详细子任务附加限制及分值如下表所示。 | 子任务 | 分值 | 约束 | | :----------: | :----------: | :----------: | |$1$|$23$|$N \leq 500$| |$2$|$35$|$N \leq 5000$| |$3$|$31$|$x_{2} - x_{1} = 1$| |$4$|$61$|无附加限制|