P12613 [CCC 2025 Junior] Connecting Territories
题目背景
本题满分 15 分。
题目描述
Ava 正在一个由格子组成的网格上玩策略游戏。每个格子都有一个对应的花费。当从左到右逐行读取格子的花费时,会呈现一个由前 $M$ 个正整数按递增顺序重复组成的模式:$1, 2, 3, \dots , M, 1, 2, 3, \dots , M, 1, 2, 3, \dots$。在这个模式中,$M$ 表示格子的最大花费。在示例网格中,$M$ 等于 $5$。
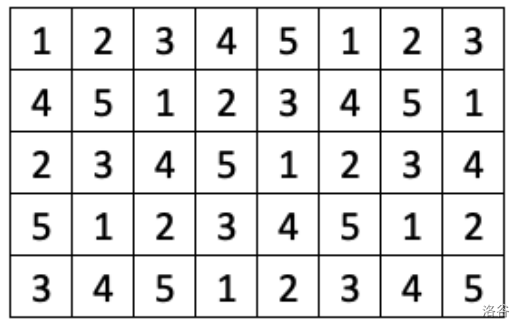
Ava 需要在每一行购买一个格子,以构建一条从上领地(第一行格子上方)通往下领地(最后一行格子下方)的连通路径。第一个购买的格子必须在第一行。随后购买的每个格子必须与上一个购买的格子共享一条边或一个角。在示例网格中,Ava 的连通路径总花费为 $9$。
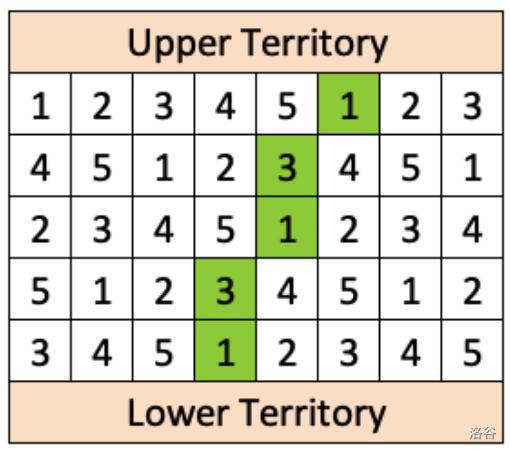
给定一个格子网格,你的任务是确定从上领地到下领地的连通路径的最小花费。
输入格式
第一行输入一个正整数 $R$,表示网格的行数。第二行输入一个正整数 $C$,表示网格的列数。第三行输入一个正整数 $M$($M \leq 100\,000$),表示格子的最大花费。
输出格式
输出一个正整数 $P$,表示连通路径的最小花费。
说明/提示
**样例输入输出解释**
每个格子的花费如图所示。Ava 应购买的格子序列(绿色高亮部分)使得连通路径的花费最小。
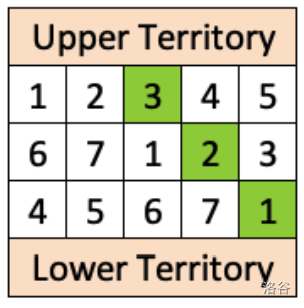
以下表格展示了 15 分的分配情况:
|分值|描述|数据范围|
|:-:|:-:|:-:|
|3|网格有两行且最多十列。|$R = 2$ 且 $C \leq 10$|
|8|网格最多十行且最多十列。|$R \leq 10$ 且 $C \leq 10$|
|2|网格最多 100 行且最多 100 列。|$R \leq 100$ 且 $C \leq 100$|
|2|网格可能非常大。|$R \leq 20\,000$ 且 $C \leq 20\,000$|
翻译由 DeepSeek V3 完成