P12617 [RMI 2023] Circles

翻译来自 [LibreOJ](https://loj.ac/p/4802)。

历史上最为顽皮的两位达契亚人——丹尼洛和斯特加诺突发奇想，决定挖一些毫无用处的隧道来捉弄后人。他们知道，未来的历史学家们会为这些莫名其妙的隧道绞尽脑汁，试图猜测它们的用途，可实际上，这些隧道压根儿没啥用。 他们找到一面巨大的墙，打算在这上面开挖。可惜的是，墙上有些地方坚不可摧，他们只能绕开这些区域。为了美观，隧道的入口必须是圆形的。 具体来说，这面墙可以看作一个笛卡尔平面，$x$ 坐标范围是 $[0, M]$，$y$ 坐标范围是 $[0, N]$。那些坚不可摧的部分是边长为 $1$ 的正方形，边与坐标轴平行，顶点位于整数坐标上。可挖掘区域的地图可以用一个二进制矩阵表示，矩阵有 $N$ 行（从 $0$ 到 $N-1$ 编号）和 $M$ 列（从 $0$ 到 $M-1$ 编号）。如果矩阵中第 $l$ 行第 $c$ 列的元素是 $1$，那么所有满足 $c \leq x \leq c+1$ 且 $l \leq y \leq l+1$ 的点 $(x, y)$ 都可以被挖开。**注意区分平面中的坐标 $(x, y)$ 和矩阵中元素的位置 $(l, c)$。** 挖隧道时，他们会先选一个**整数坐标** $(x, y)$ 作为隧道的中心，然后确定一个半径 $r$，接着开始挖掘以 $(x, y)$ 为圆心、半径为 $r$ 的圆盘内的所有点。**注意，这个圆盘包括内部的所有点，不仅仅是圆周上的点，而且圆盘必须完全位于定义的平面内。** 他们希望隧道越显眼越好，所以想挖一个半径最大的隧道。为了施工方便，如果有多个半径最大的隧道，他们会挑一个最好挖的——也就是 $y$ 坐标最小的那个。如果还有多个选择，他们就选 $x$ 坐标最小的那个。

第一行包含两个整数 $N$ 和 $M$，分别表示定义平面的范围和二进制矩阵的尺寸。 接下来的 $N$ 行，每行是一个长度为 $M$ 的字符串，由 `0` 和 `1` 组成，表示上面定义的矩阵元素。

在一行中输出三个用空格分隔的整数 $x, y, R$。$(x, y)$ 表示丹尼洛和斯特加诺将要挖掘的隧道中心的坐标，$R$ 表示圆的半径平方后取整的结果。如果找不到半径为正整数的圆，输出 `0 0 0`。

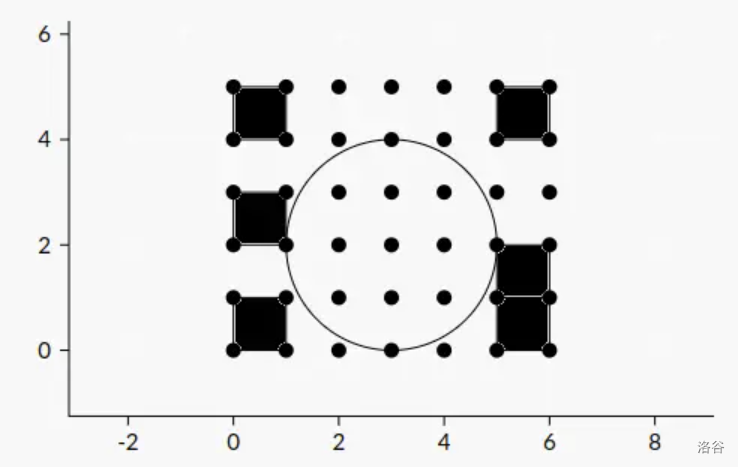
### 样例 1 解释  ### 数据范围与提示 对于所有输入数据，满足： * $1 \leq N, M \leq 3\ 000$ 详细子任务附加限制及分值如下表所示。 | 子任务 | 分值 | 附加限制 | | :---: | :---: | :--: | | $1$ | $4$ | 矩阵中恰好有四个格子是 $1$。| | $2$ | $9$ | 矩阵中的 $1$ 构成一个边与坐标轴平行的矩形。 | | $3$ | $14$ | $N, M \leq 50$ | | $4$ | $15$ | $N, M \leq 600$ | | $5$ | $21$ | 矩阵是随机生成的。 | | $6$ | $37$ | 无附加限制 |