P12619 [RMI 2023] To be, xor not to be

翻译来自 [LibreOJ](https://loj.ac/p/4804)。

丹德罗马克的贵族王子斯特甘，因心爱的父亲去世而悲痛万分。他曾不懈地尝试通过计算各种梯形图形的面积（用辛普森法则）来探究父亲的命运，可惜毫无结果。正当他几近绝望时，一位精灵现身相助，赠予他一棵树，让他悉心照料。后来，精灵对他说：「看！仔细看！你发现了吗？这棵树很特别，它的顶点数量是偶数。只要你能找到一种最佳方式，把这些顶点两两配对，让配对的总成本尽可能小，你就能揭开父亲去世的真相。不过，首先你得弄清楚配对的成本是什么，它的秘密藏在生命的意义里。」 斯特甘是个数学天才，他深知生命的真谛在于那句名言：「生存，**还是异或生存**」（至于后面的话，咱们就不多说了）。于是他推断出，对于一对顶点，配对的成本是连接它们的简单路径上所有边的权值的按位异或（XOR）结果。 可惜，天意弄人，斯特甘完全不懂计算机科学，面对这个问题束手无策，只好向你求助。 具体来说，你会得到一棵有 $N$ 个顶点的树，$N$ 是偶数。每条边都有一个权值。对于一对顶点 $(u, v)$，它们的配对成本是连接它们的简单路径上所有边权值的按位 XOR。 你的任务是把这些顶点分成 $\frac{N}{2}$ 对，使得所有配对成本的总和尽量小。因为要找到绝对的最优解可能太难，我们只要求你尽力而为，你会根据结果获得相应的分数。

第一行是一个偶数整数 $N$，表示树中顶点的数量。接下来的 $N-1$ 行，每行包含三个用空格分隔的数字 $u_i, v_i, w_i$，表示有一条权值为 $w_i$ 的边连接 $u_i$ 和 $v_i$。$u_i$ 和 $v_i$ 都在 $1$ 到 $N$ 之间。

第一行输出你所选配对的总成本。接下来的 $\frac{N}{2}$ 行，每行输出一对配对的顶点编号。所有配对之间不能有重复的顶点。

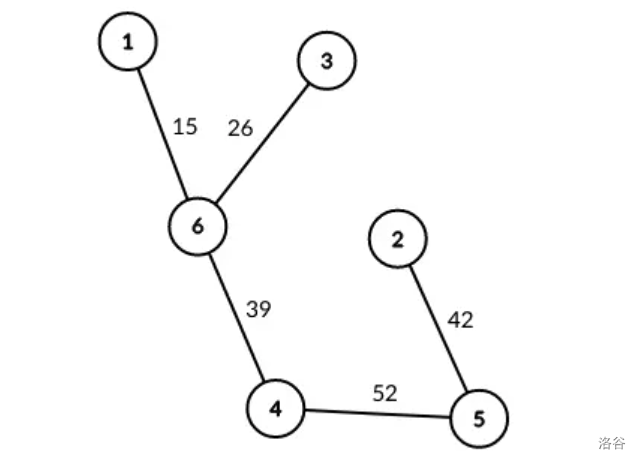
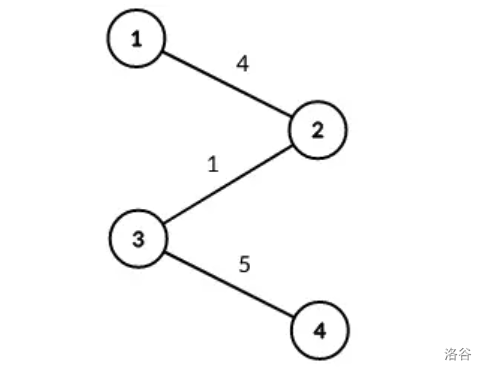
### 样例 1 解释  ### 样例 2 解释  ### 数据范围与提示 对于所有输入数据，满足： * $2 \leq N \leq 200$ * $N$ 是偶数 * $0 \leq w_i \leq 2^{24}$ * 按位 XOR (^) 操作返回一个数字，其二进制表示中，每一位上是 $1$ 的情况是两个操作数对应位中恰好有一个是 $1$。 详细子任务附加限制及分值如下表所示。 | 子任务 | 分值 | 附加限制 | | :---: | :---: | :--: | | $1$ | $3$ | $N \leq 10, w_i \leq 64$| | $2$ | $6$ | $N \leq 14$ | | $3$ | $19$ | $N \leq 40, w_i \leq 64$| | | $4$ | $8$ | $N \leq 120, w_i \leq 16$| | | $5$ | $41$ | $N \leq 120$ | | $6$ | $23$ | 无附加限制 | 对于每个子任务： 1. 如果你的程序在某个测试点中无法生成有效答案（超时、运行错误），该子任务得分为 $0$。 2. 如果你输出的 $\frac{N}{2}$ 对配对无法正确分割 $N$ 个顶点，或者与你输出的总成本不符，答案也不算正确。 3. 如果以上情况都没发生，你将根据以下公式得分： $$\text{group\_score} \cdot \min \left\{ \left( \frac{ok\_cost_i}{out\_cost_i} \right) ^4 \right\}$$ 其中： * $i$ 表示该子任务中的每个测试点 * $out\_cost_i$ 是你的代码在测试点 $i$ 中计算出的成本 * $ok\_cost_i$ 是测试点 $i$ 的最优答案