P12631 [ICPC 2025 NAC] Solar Farm

You are building a new solar farm. The area in which you are allowed to build is a circular field of radius $r$, and the solar panels each take up a rectangular space of size $w \times h$. You must place all the panels in the same orientation of your choice in a single rectangular array (so that all of the panels combined exactly form a single rectangle). What is the maximum number of panels that you can fit in this farm?

The first line of input contains a single integer $T$ ($1\leq T \leq 1\,000$). This is the number of test cases. The next $T$ lines of input each represent one test case and consist of three space-separated integers $r$, $w$, and $h$ ($1 \leq r, w, h \leq 10^9$): the radius of the field, the width of each solar panel, and the height of each solar panel, respectively.

For each test case, print a line with a single integer: the maximum number of solar panels that can be placed in a solar farm within the circular field.

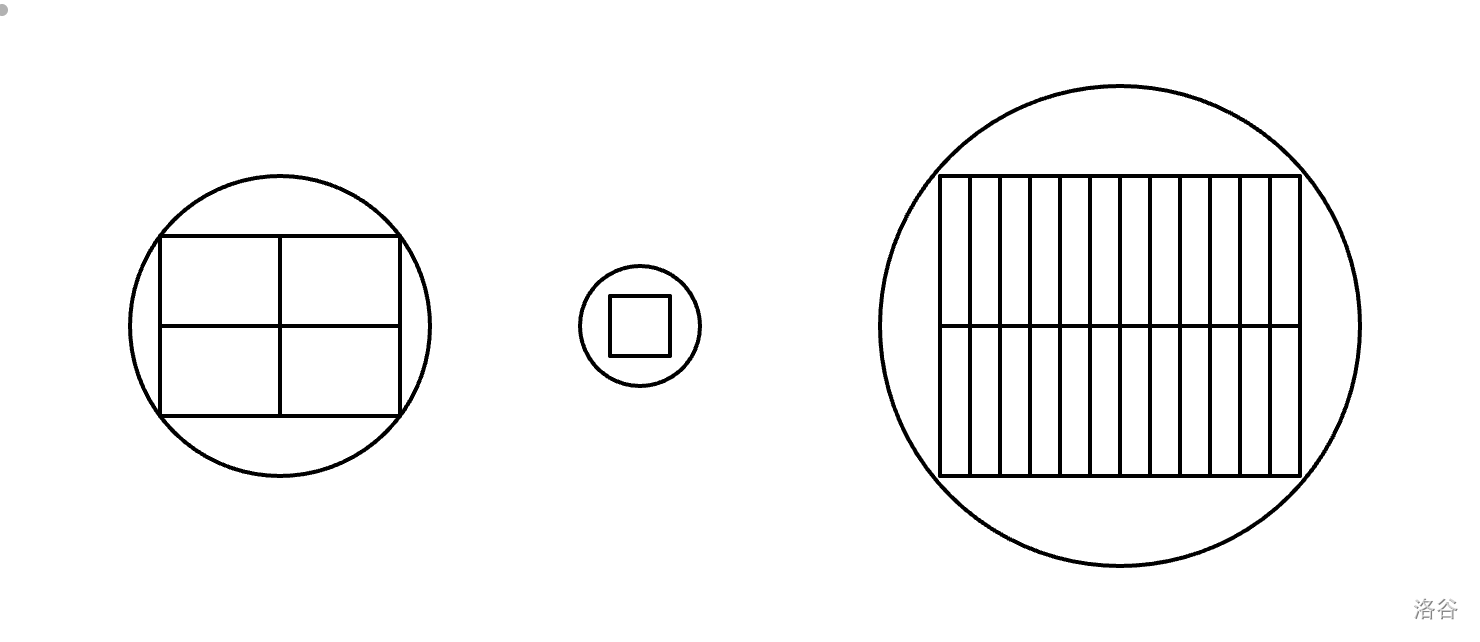
The diagram below illustrates one optimal layout of solar panels for each of the three test cases in Sample Input 1 (from left to right).