P12645 [KOI 2024 Round 1] 二叉树

试题来源：。中文翻译做了少量本土化修改。 按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。

对于所有子节点个数为 $0$ 或 $2$ 的二叉树 $T$，定义 $S(T)$ 的值如下： - 对于 $T$ 中某个节点 $u$，以 $u$ 为根的子树是仅包含 $u$ 和 $u$ 的所有后代节点的集合。 - $T$ 的中序遍历序列 $p(T)$ 是按照中序遍历方式访问节点所得到的序列，其定义如下： - 设 $r$ 为 $T$ 的根节点。记 $[r]$ 为仅包含 $r$ 的长度为 $1$ 的序列。 - 若 $r$ 没有子节点，则 $p(T) = [r]$； - 若 $r$ 有两个子节点，设以 $r$ 的左子节点为根的子树为 $X$，右子节点为根的子树为 $Y$，则有 $p(T) = p(X), [r], p(Y)$，按此顺序拼接而成。 - 设 $T$ 的叶子节点数为 $k$。将编号 $1, 2, \dots, k$ 按照这些叶子节点在 $p(T)$ 中出现的顺序赋予它们。 - 若选择了一个子树，该子树中包含的所有叶子节点就被称为“被覆盖”。 - 对于 $1 \leq a \leq b \leq k$，定义 $f(a, b)$ 为为了只覆盖编号在 $[a, b]$ 区间内的叶子节点而不覆盖其他叶子节点所需选择的最少子树个数。 - $S(T)$ 的值为所有满足 $1 \leq a \leq b \leq k$ 的整数对 $(a, b)$ 的 $f(a, b)$ 之和对 $10^9 + 7$ 取模的结果。 例如，假设给定一个如图所示的二叉树 $T$，则 $f(5, 7)$ 的值为 $2$，因为可以通过选择两个子树来仅覆盖 $5$、$6$ 和 $7$ 号叶子节点。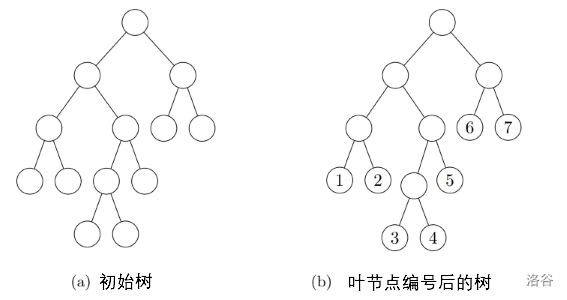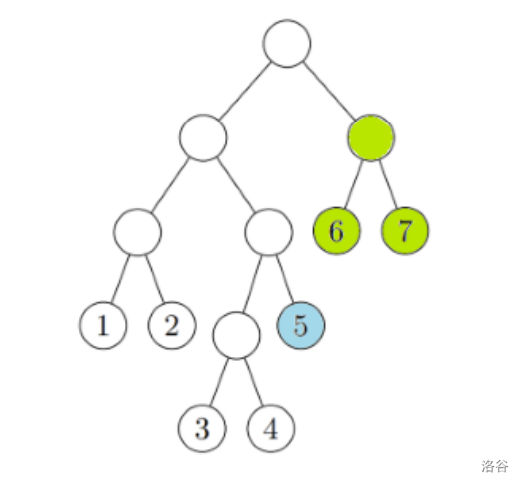   根据上述方式，对所有 $1 \leq a \leq b \leq 7$ 的 $f(a, b)$ 求和得到 $47$，因此 $S(T) = 47 \bmod (10^9 + 7)$。 给定两个整数序列 $A_1, A_2, \dots, A_N$ 和 $B_1, B_2, \dots, B_N$，定义一系列二叉树 $T_0, T_1, \dots, T_N$ 如下： - $T_0$ 为仅包含一个节点的树； - 对于 $1 \leq i \leq N$，$T_i$ 是一个二叉树，其左子树为 $T_{A_i}$，右子树为 $T_{B_i}$。 请编写程序，求出 $S(T_1), S(T_2), \dots, S(T_N)$。

第一行输入一个整数 $N$。 接下来 $N$ 行，每行输入两个整数 $A_i$ 和 $B_i$，以空格分隔。

输出 $N$ 行，第 $i$ 行输出 $S(T_i)$ 的值。

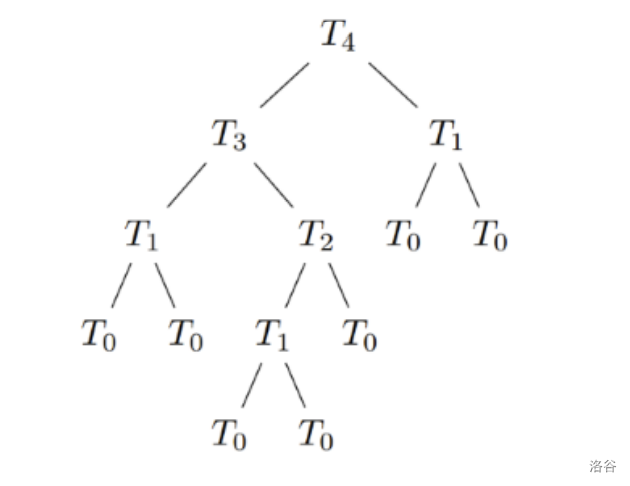
**样例 1 解释** 示例中的 $T_4$ 如下图所示。  **约束条件** - 所有输入均为整数。 - $1 \leq N \leq 100\,000$ - $0 \leq A_i \leq i - 1\ (1 \leq i \leq N)$ - $0 \leq B_i \leq i - 1\ (1 \leq i \leq N)$ **子问题** 1. （5 分）$A_i = B_i = i - 1\ (1 \leq i \leq N),\ N \leq 10$ 2. （10 分）$A_i = B_i = i - 1$ 3. （5 分）$A_i = i - 1,\ B_i = 0$ 4. （10 分）所有 $T_1, \dots, T_N$ 的节点总数不超过 $1\,000$ 5. （25 分）所有 $T_1, \dots, T_N$ 的节点总数不超过 $300\,000$ 6. （45 分）无额外限制条件 翻译由 ChatGPT-4o 完成