P12647 [KOI 2024 Round 2] 寻宝游戏

试题来源：。中文翻译做了少量本土化修改。 按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。

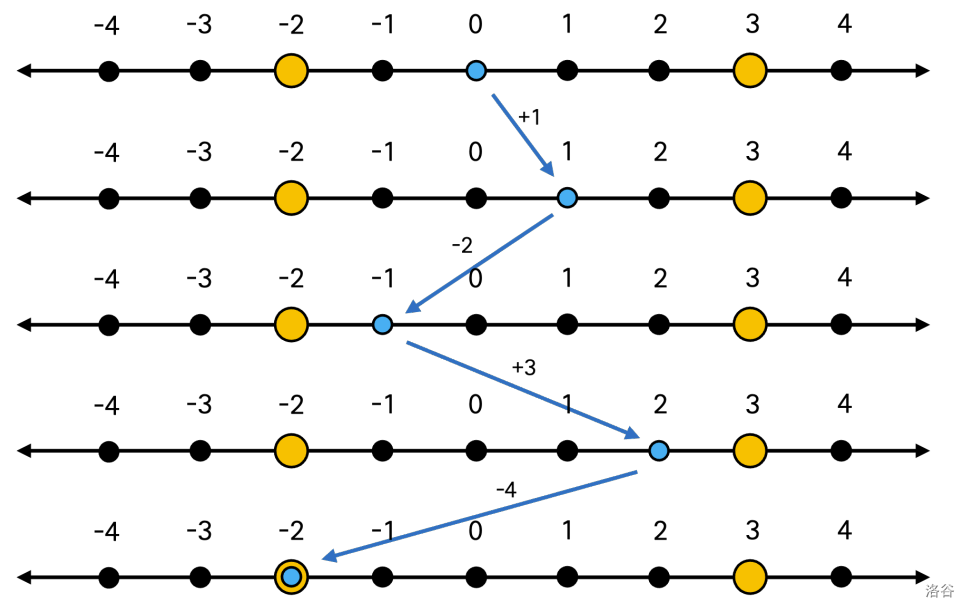
你正与朋友小彬在如下图所示的无限长数轴上玩寻宝游戏。  首先，你会将两件宝物藏在数轴上两个不同的位置 $L$ 和 $R$ 上（满足 $L < R$）。下图为将宝物藏在 $L = -2$ 和 $R = 3$ 的一个例子。用橙色标示的两个格子中藏有宝物。  你藏好宝物后，小彬便开始找宝物。她将从你指定的起始位置 $S$ 出发，按照以下顺序进行： - 第一步：检查当前位置 $S$； - 第二步：向右移动 $1$ 格，检查位置 $S + 1$； - 第三步：向左移动 $2$ 格，检查位置 $S + 1 - 2$； - 第四步：向右移动 $3$ 格，检查位置 $S + 1 - 2 + 3$； - 第五步：向左移动 $4$ 格，检查位置 $S + 1 - 2 + 3 - 4$； - 第六步：向右移动 $5$ 格，检查位置 $S + 1 - 2 + 3 - 4 + 5$； - … 也就是说，第 $x$ 步时，如果 $x$ 是偶数，小彬会向右移动 $x - 1$ 格；如果 $x$ 是奇数，小彬会向左移动 $x - 1$ 格，然后检查所到达的位置。 如果某一步检查的位置上有宝物，游戏就结束。 例如，在 $L = -2$、$R = 3$、$S = 0$ 的情形下，小彬会在第 $5$ 步检查位置 $-2$，那里藏有宝物，因此游戏会在第 $5$ 步结束。 

第一行输入一个整数 $T$，表示你想测试的游戏情况数。 接下来 $T$ 行，每行三个整数 $L\ R\ S$，表示两个宝物的位置 $L,\ R$ 和小彬的起始位置 $S$。

输出 $T$ 行，第 $i$ 行输出对应第 $i$ 个游戏中，游戏在第几步结束（即找到第一个宝物）。

**样例 1 说明** - 第一个例子如题面图所示，小彬第 $5$ 步找到了位置 $-2$ 的宝物。 - 第二个例子中，小彬从 $6$ 出发： - 第 1 步：$6$ - 第 2 步：$7$ - 第 3 步：$5$ - 第 4 步：$8$ ← 找到宝物，游戏结束。 **约束条件** - 所有输入为整数。 - $1 \leq T \leq 10\,000$ - $-100\,000\,000 \leq L < S < R \leq 100\,000\,000$ **子问题** 1. （8 分）$T = 1,\ R = 1,\ S = 0$ 2. （9 分）$T = 1,\ L = -1,\ S = 0$ 3. （15 分）$-1\,000 \leq L \leq -1,\ 1 \leq R \leq 1\,000,\ S = 0$ 4. （16 分）$-1\,000 \leq L < S < R \leq 1\,000$ 5. （52 分）无额外限制条件 翻译由 ChatGPT-4o 完成