P12652 [KOI 2024 Round 2] 拔树游戏

试题来源：。中文翻译做了少量本土化修改。 按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。

有一棵由编号为 $1$ 到 $N$ 的 $N$ 个节点构成的有根树。该树的根节点为 $1$ 号节点，并且第 $i$ 号节点的父节点是第 $P_i$ 号节点（$2 \le i \le N$）。此外，每个节点都有一个互不相同的整数权值，第 $i$ 号节点的权值为 $A_i$（$1 \le i \le N$）。 不含子节点的节点称为叶子节点。 我们从根节点（即 $1$ 号节点）出发，每次移动到当前节点的子节点中权值最小的一个。如此重复，直到到达某个叶子节点。这样得到的从 $1$ 号节点出发、以某个叶子节点结束的路径，记作 $S = \{S_1, S_2, \ldots, S_k\}$，我们称其为**特殊路径**。 定义**拔除操作**如下： - 设当前树的特殊路径为 $S = \{S_1, S_2, \ldots, S_k\}$。 - 将 $S_1$ 与 $S_2$ 的权值交换。 - 将 $S_2$ 与 $S_3$ 的权值交换。 - 依此类推…… - 将 $S_{k-1}$ 与 $S_k$ 的权值交换。 - 从树中移除连接 $S_k$ 与其父节点之间的边。 换句话说，拔除操作会将特殊路径上的节点的权值依次向后传递，并将该路径最后一个叶子节点从树中删除。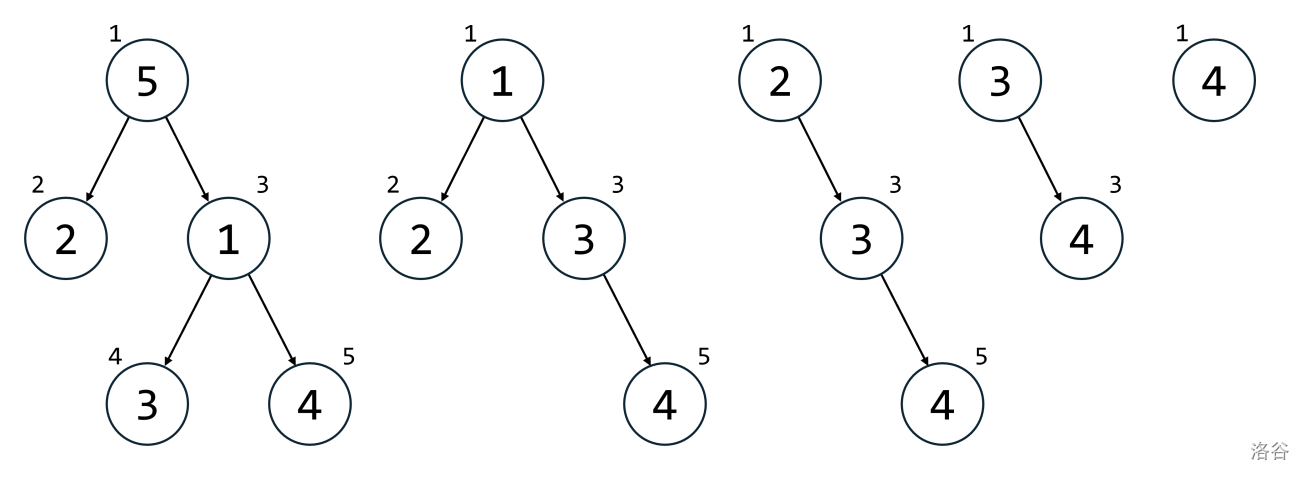 例如，考虑下图中的树（图中圆圈外的数字表示节点编号，圆圈内的数字表示该节点的权值）：  在第一棵树中，特殊路径为 $S = \{1, 3, 4\}$：从根节点 $1$ 出发，子节点中权值最小的是 $3$ 号节点，再从 $3$ 出发，选择子节点中权值最小的 $4$，$4$ 是叶子节点，结束路径。 进行拔除操作后，依次交换权值 $A_1 \leftrightarrow A_3$，$A_3 \leftrightarrow A_4$，并删除 $4$ 与 $3$ 之间的边，得到第二棵树。 在第二棵树中，特殊路径为 $S = \{1, 2\}$：$1$ 的子节点中权值最小的是 $2$，$2$ 是叶子节点。进行拔除操作，交换 $A_1 \leftrightarrow A_2$，删除 $2$ 与 $1$ 的边，得到第三棵树。 在第三棵树中，特殊路径为 $S = \{1, 3, 5\}$。拔除操作为交换 $A_1 \leftrightarrow A_3$，$A_3 \leftrightarrow A_5$，然后删除 $5$ 与 $3$ 之间的边，得到第四棵树。 在第四棵树中，特殊路径为 $S = \{1, 3\}$。执行拔除操作后交换 $A_1 \leftrightarrow A_3$，再删除 $3$ 与 $1$ 的边，得到第五棵树。 在第五棵树中，特殊路径仅为 $S = \{1\}$。执行拔除操作后，直接删除根节点 $1$。 我们将对给定的树重复执行 $N$ 次拔除操作。请你编写一个程序，在每次拔除操作执行**之前**，输出当前 $1$ 号节点的权值。

第一行输入一个整数 $N$，表示节点个数。 第二行输入 $N-1$ 个整数 $P_2, P_3, \ldots, P_N$，表示每个节点的父节点编号，数字之间以空格分隔。 第三行输入 $N$ 个整数 $A_1, A_2, \ldots, A_N$，表示每个节点的初始权值，数字之间以空格分隔。

输出共 $N$ 行，每行一个整数，第 $i$ 行表示执行第 $i$ 次拔除操作**之前**，$1$ 号节点的权值。

**约束条件** - 所有给定数值均为整数。 - $2 \le N \le 300\,000$ - $1 \le P_i < i \quad (2 \le i \le N)$ - $1 \le A_i \le N \quad (1 \le i \le N)$ - 所有 $A_i$ 两两不同。 **子任务** 1. （6 分）$N \le 3\,000$ 2. （10 分）对所有 $2 \le i \le N$，有 $A_{P_i} < A_i$ 3. （11 分）对所有 $2 \le i \le N$，有 $A_{P_i} > A_i$ 4. （23 分）度数大于等于 $3$ 的节点个数不超过 $20$ 5. （50 分）无额外限制 翻译由 ChatGPT-4o 完成