P12658 [KOI 2023 Round 1] 格子游戏

试题来源：。中文翻译做了少量本土化修改。 按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。

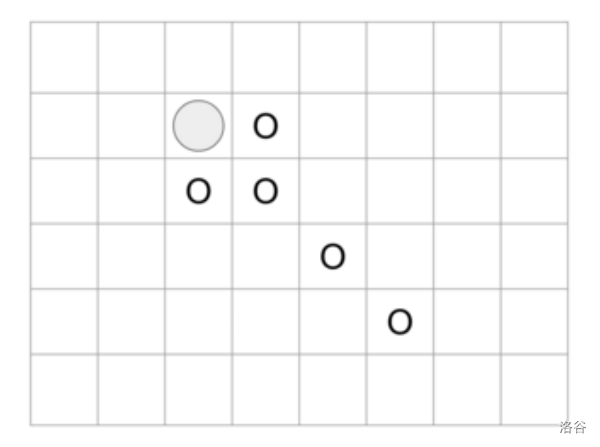
韩果和正奥在一个格子状的棋盘上轮流移动棋子进行游戏，韩果先手。不能跳过自己的回合。 棋盘由 $N$ 行 $M$ 列构成，部分格子被封锁，不能移动到这些格子上。为方便起见，记从上往下的第 $i$ 行与从左往右的第 $j$ 列交汇的格子为 $(i, j)$。 棋子每次可以向下移动一格、向右移动一格，或者沿右下方向移动 $1$ 到 $K$ 格（即 $(1, 1)$ 到 $(K, K)$ 的任意一个方向）。但不能移动出棋盘或进入封锁格子中。如果 $K = 0$，则不能进行对角线方向的移动。 我们来看看与移动规则相关的几个例子： 假设 $N = 6$，$M = 8$，$K = 3$，且棋盘上没有封锁的格子。此时位于 $(2, 3)$ 的棋子可移动到的格子共有 5 个，如下图用 O 表示。  如果再假设 $(2, 4)$ 和 $(4, 5)$ 是封锁格子，那么位于 $(2, 3)$ 的棋子可移动到的格子变成 3 个，如图所示。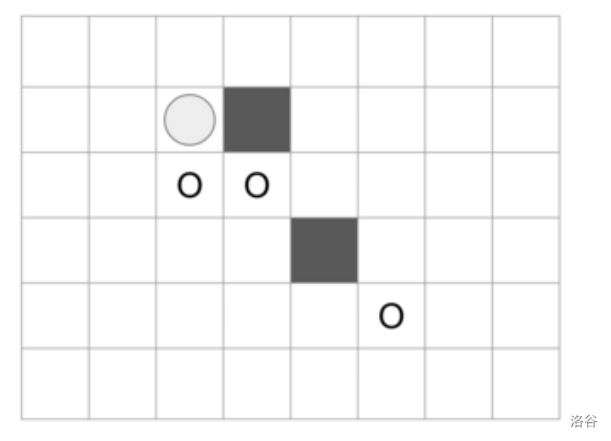  接下来我们再看两个示例： - 若棋子位于 $(5, 7)$，$N = 6$，$M = 8$，$K = 3$，无封锁格子，则可以移动到的格子数为 $3$，如图所示。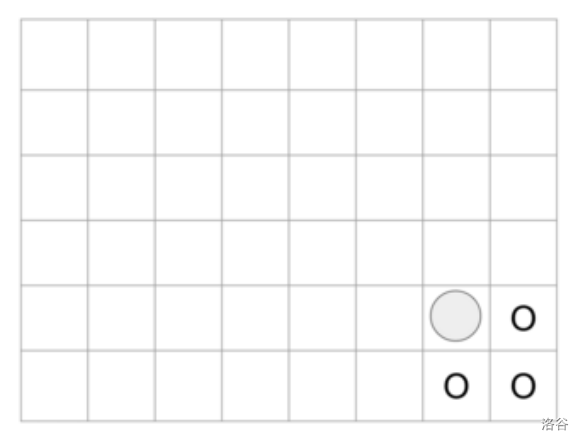  - 若棋子位于 $(1, 1)$，$K = 0$，无封锁格子，则可移动到的格子为 $2$ 个，如图所示。  游戏的目标是将棋子移动到棋盘最右下角的格子，即 $(N, M)$。最后一个完成移动的人获胜。假设韩果和正奥都会以最优策略进行游戏。 游戏的胜负与初始位置有关。给出 $Q$ 个初始位置 $(x_1, y_1), (x_2, y_2), \dots, (x_Q, y_Q)$，请判断从这些位置开始游戏，谁将获胜。

第一行包含三个整数 $N$、$M$ 和 $K$，用空格隔开。 接下来 $N$ 行，每行一个长度为 $M$ 的仅包含 `#` 或 `.` 的字符串，表示棋盘状态。若为 `#` 表示该格为封锁格子，`.` 表示可通行。 然后是一个整数 $Q$。 接下来的 $Q$ 行中，每行两个整数 $x_i$ 和 $y_i$，表示游戏起始位置。

对每个起始位置，若韩果（先手）能赢，输出 `First`；若正奥（后手）能赢，输出 `Second`。每个结果占一行，按输入顺序输出。

**限制条件** - 所有给定值均为整数。 - $2 \leq N \leq 300$ - $2 \leq M \leq 300$ - $K \geq 0$ - $K \leq N - 1$ - $K \leq M - 1$ - $(N, M)$ 不是封锁格子。 - 从任意未封锁格子出发，根据规则都可以到达 $(N, M)$。 - $1 \leq Q \leq 300$ - 对于每个 $1 \leq i \leq Q$： - $1 \leq x_i \leq N$，$1 \leq y_i \leq M$ - $(x_i, y_i)$ 是未封锁格子，且不等于 $(N, M)$ **子问题** 1. （5 分）$K = 0$ 2. （17 分）$N = M$ 且 $K \geq 1$，满足 $i \ne j$ 的格子均为封锁格子。 3. （25 分）无封锁格子。 4. （53 分）无额外限制。 翻译由 ChatGPT-4o 完成