P1268 Weight of a Tree

Trees can be used to represent evolutionary relationships among species. An "evolutionary tree" is a tree with edge weights, where each leaf node represents a species, and the distance between two leaves represents the difference between the two species. Now, an important problem is to reconstruct the corresponding "evolutionary tree" from the distances between species. Let $N=\{1,2,3,\cdots ,n\}$, and use a matrix $M$ on $N$ to define a tree $T$. The matrix $M$ satisfies: for any $i$, $j$, $k$, we have $M[i,j]+M[j,k] \ge M[i,k]$. The tree $T$ satisfies: 1. The leaves are the elements of $N$. 2. All edge weights are non-negative integers. 3. $d_T(i,j)=M[i,j]$, where $d_T(i,j)$ denotes the length of the shortest path between $i$ and $j$ in the tree. 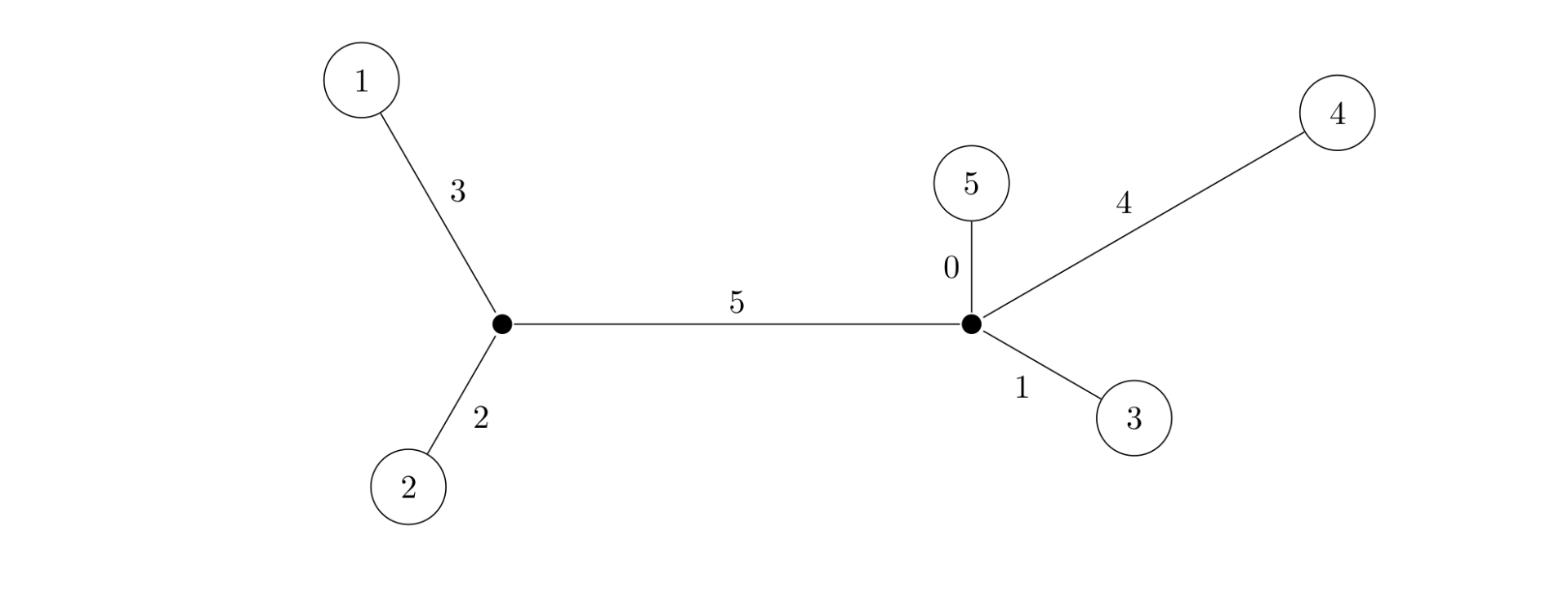As shown below, the matrix $M$ describes a tree. $$M=\begin{bmatrix} 0 & 5 & 9 & 12 & 8 \\ 5 & 0 & 8 & 11 & 7 \\ 9 & 8 & 0 & 5 & 1 \\ 12 & 11 & 5 & 0 & 4 \\ 8 & 7 & 1 & 4 & 0 \\ \end{bmatrix}$$ The weight of a tree is the sum of all edge weights in the tree. For any valid matrix $M$, the total weight of the tree it represents is uniquely determined. It is impossible to find two trees with different total weights that are both consistent with $M$. Your task is to compute the weight of the tree represented by the given matrix $M$. The figure below shows one tree represented by the above matrix $M$, and the total weight of this tree is $15$. 

The first line contains an integer $n$ with $2

Output one line containing a single integer, the total weight of the tree.

Translated by ChatGPT 5