P1269 Signal Amplifier

A tree network minimizes material use. A tree network is an acyclic connected network in which there is exactly one communication path between any two nodes. There is one node in the network that is the server, responsible for sending a signal directly or indirectly to all terminals. As shown in the top figure, the server node sends a signal to nodes $a$ and $c$, and $a$ then forwards it to $b$. In this way, the entire network receives the signal.  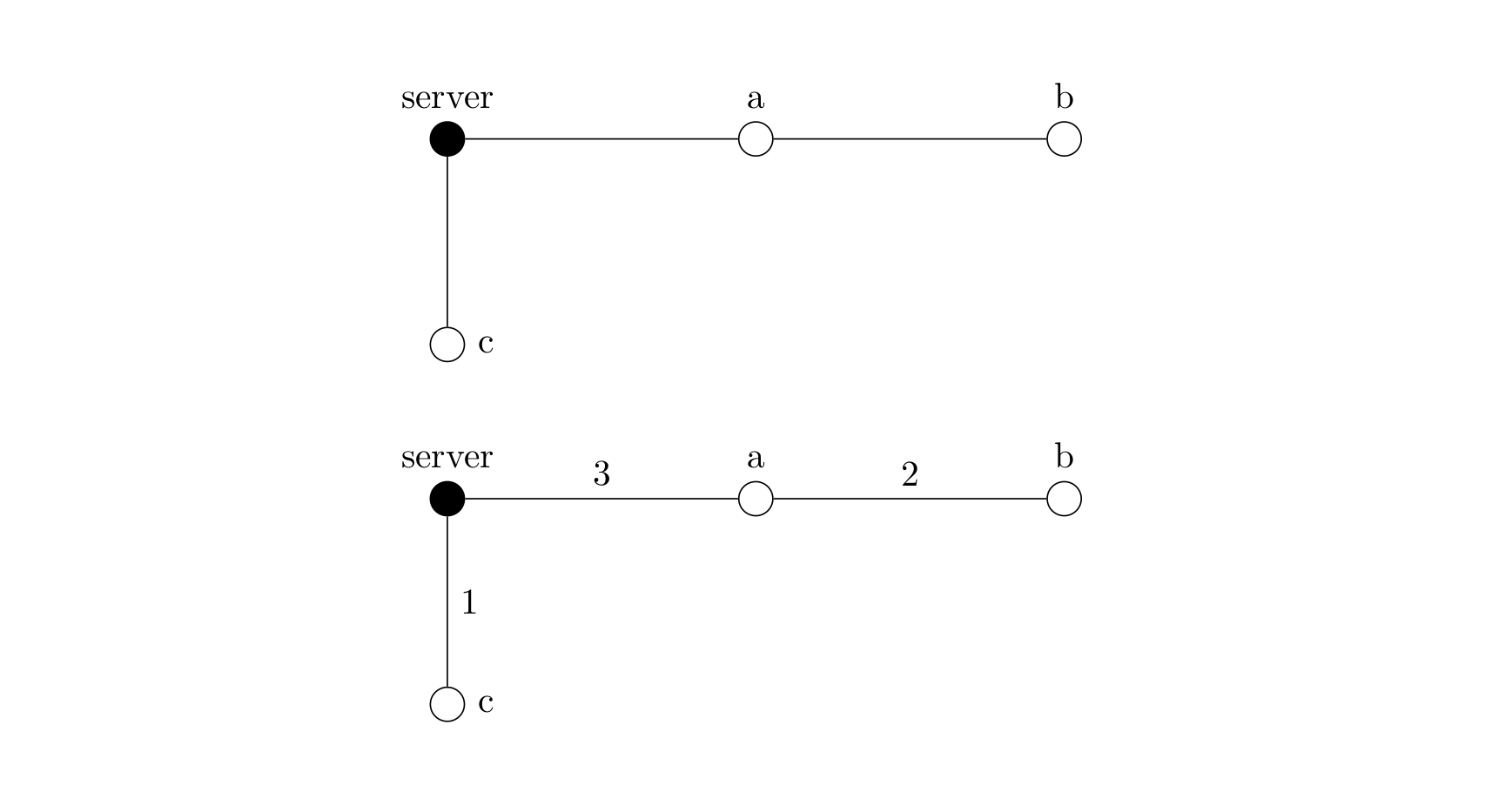However, in practice, when a signal is sent from one node to another, its strength attenuates. The attenuation is generally determined by the length of the line. As shown in the bottom figure, the numbers on the edges indicate the attenuation on those edges. Suppose a signal of strength $4$ units is emitted from the server; after reaching node $a$, the strength attenuates to $4-3=1$ unit. Node $a$ then forwards it to node $b$. Since the signal strength is $1$ and the attenuation is $2$, the signal cannot be delivered to $b$. One way to solve this problem is to install signal amplifiers. A signal amplifier restores any signal with positive strength to the initial strength (the strength at the server when it is emitted). In the figure above, if a signal amplifier is installed at node $a$, then when the signal of strength $4$ reaches $a$, it is amplified back to $4$. Thus, the signal can be delivered to any node in the network. To simplify the problem, we assume each node processes a signal at most once; when it receives the same signal a second time, it ignores it. Your task is to compute, for the given tree network, the minimum number of signal amplifiers that must be installed.

The first line contains an integer $n$, the number of nodes in the network ($n \le 20000$). Lines $2$ to $n+1$ each describe the connections of a node. Specifically, line $i+1$ describes node $i$: it starts with an integer $k$, the number of nodes adjacent to node $i$. Then follow $2k$ numbers, where each pair describes a neighbor of node $i$: the neighbor’s identifier (an integer between $1$ and $n$) and the attenuation on the edge between that neighbor and node $i$. Node $1$ is the server. The last line contains one integer, the initial signal strength emitted by the server.

Output a single integer, the minimum number of signal amplifiers required to make the signal reach the entire network. If it is impossible to make the signal reach the entire network no matter how the amplifiers are installed, output `No solution.`.

Translated by ChatGPT 5