P12703 [KOI 2022 Round 2] 外环路
题目背景
试题来源:。中文翻译做了少量本土化修改。
按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。
题目描述
KOI 城市由 $N$ 个十字路口和 $N - 1$ 条双向道路组成,任意两个不同的十字路口之间都可以仅通过道路到达。也就是说,城市的道路网络结构是一棵树。这些道路位于二维平面上,除了端点外互不相交。每条道路都有一个不小于 0 的整数权重,表示通过这条道路所需的时间。
KOI 城市在几十年前还是一个小村庄,随着人口流入和城市规模的迅速扩张,市长为了行政便利,为所有十字路口编号为 1 到 $N$。这个编号系统满足以下性质:
- 1 号十字路口是城市的中心,保证至少连接了两条道路。
- 各个十字路口的编号是以 1 号十字路口为根进行先序遍历(Preorder Traversal)所得到的一种顺序。
- 对于每个十字路口,设其直接相邻(即通过一条道路连接)的十字路口中编号最小的为基准,从该点出发按逆时针方向依次列出其相邻的十字路口编号,这些编号应是递增的。
随着 KOI 城市人口迅速增长,交通拥堵问题日益严重。为了解决这一问题,市长决定通过建设外环道路将交通设施最为薄弱的地区连接起来。
设所有仅连接一条道路的十字路口的编号按升序排列为 $\{v_1, v_2, \dots, v_k\}$,市长将为所有的 $1 \leq i \leq k$ 建设一条连接 $v_i$ 和 $v_{(i \bmod k) + 1}$ 的双向道路。每条道路的权重为不小于 0 的整数 $w_i$,这些权重将作为输入给出。
由于编号系统的特殊性,可以保证这些新增的外环道路在非端点处互不相交。
你打算为 KOI 城市构建一套导航系统。该系统需要回答 $Q$ 个查询,每个查询给出两个十字路口 $u$ 和 $v$,你需要输出从 $u$ 号十字路口到 $v$ 号十字路口所需的最短时间。这个最短时间是指从 $u$ 到 $v$ 所经过路径的所有道路权重之和的最小值。
请你编写程序,在给定城市道路结构和查询的前提下,快速回答所有 $Q$ 个查询。
输入格式
第一行包含一个整数 $N$,表示十字路口的数量。
接下来的 $N - 1$ 行,第 $i$ 行包含两个整数 $p_i$ 和 $c_i$,表示存在一条连接 $p_i$ 和 $i+1$ 的双向道路,权重为 $c_i$。
设整数 $k$ 表示仅连接一条道路的十字路口的数量。
随后一行包含 $k$ 个整数 $w_1, w_2, \dots, w_k$,以空格分隔,其中 $w_i$ 是连接 $v_i$ 和 $v_{(i \bmod k)+1}$ 的新建道路的权重。
接下来一行包含一个整数 $Q$,表示查询数量。
接下来的 $Q$ 行,每行两个整数 $u, v$,表示一次从 $u$ 到 $v$ 的查询。
输出格式
共 $Q$ 行,每行一个整数,表示每个查询中 $u$ 到 $v$ 的最短路径长度。
说明/提示
**样例 1 说明**
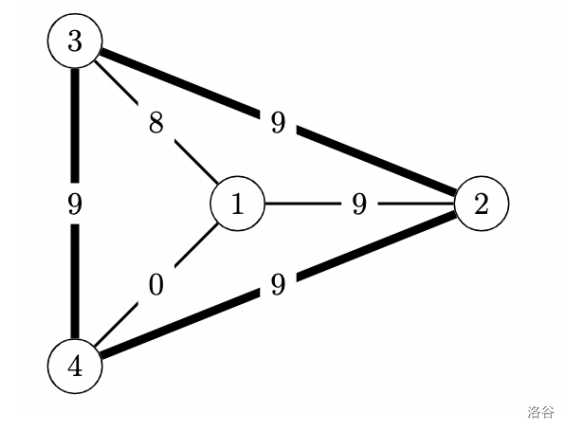
上面的地图对应于示例 1。示例 1 满足子任务 2、5、6 的约束条件。
**样例 2、3 说明**
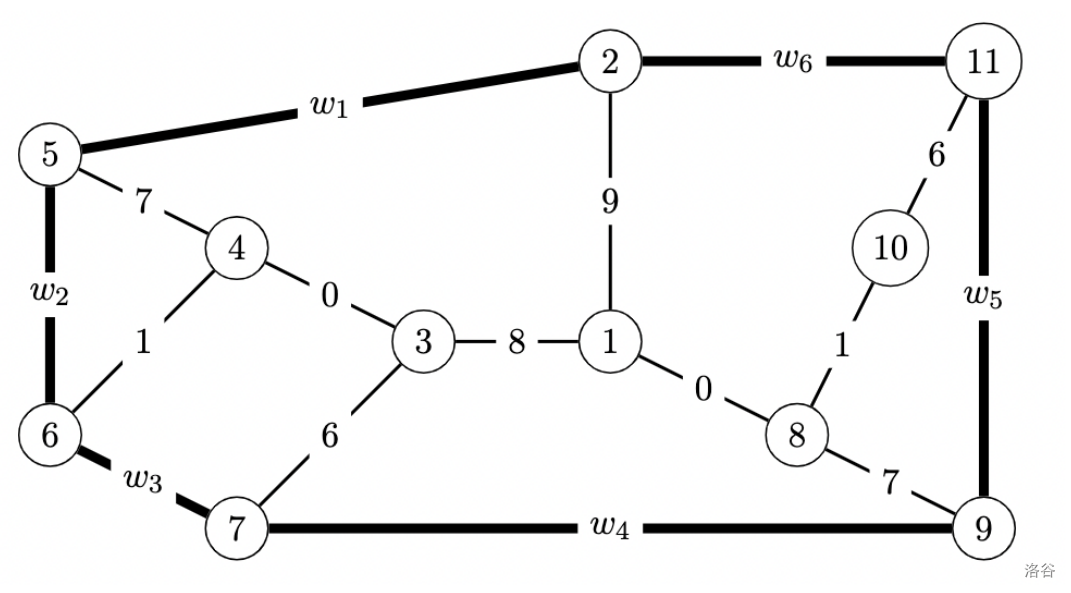
上面的地图对应于示例 2 和示例 3。示例 2 的情况下,满足 $w_i = 0$;示例 3 的情况下,满足 $w_i = 10^{12}$。示例 2 满足子任务 4、5、6 的约束条件,示例 3 满足子任务 3、5、6 的约束条件。
请注意,示例 3 中从第 12 行开始的数列:
```
1000000000000 1000000000000 1000000000000 1000000000000 1000000000000 1000000000000
```
在实际中是作为一行输入给出的,但由于篇幅限制,在此被分成了多行显示。(本段内容在正式比赛中并未提供。)
**约束条件**
- $4 \leq N \leq 100\,000$
- $1 \leq p_i \leq i$
- $0 \leq c_i, w_i \leq 10^{12}$
- $1 \leq Q \leq 250\,000$
- $1 \leq u, v \leq N$ 且 $u \ne v$
**子任务**
1. (6 分)所有查询满足 $u = 1$
2. (8 分)对所有 $1 \leq i \leq N - 1$,$p_i = 1$
3. (5 分)对所有 $1 \leq i \leq N - 1$,$c_i \leq 10^6$,并且对所有 $1 \leq i \leq k$,$w_i = 10^{12}$
4. (15 分)对所有 $1 \leq i \leq k$,$w_i = 0$
5. (57 分)不存在连接 4 条及以上道路的十字路口
6. (9 分)无额外约束条件