P12721 [KOI 2021 Round 2] 矩形面积

试题来源：。中文翻译做了少量本土化修改。 按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。

给定一张边长均为 $N$ 的大纸张。坐标 $(X, Y)$ 表示从纸张的最左上角 $(0, 0)$ 出发，竖直方向移动 $X$、水平方向移动 $Y$ 后到达的点。因此，纸张的最右下角坐标为 $(N, N)$。 现在给出 $C$ 个点。这些点的坐标都是正整数，并依次从 1 到 $C$ 编号。多个点可能具有相同的坐标。 对于编号顺序的每个点，依次进行以下操作。设当前纸张的竖直长度为 $A$，水平方向长度为 $B$，而本次处理的点坐标为 $(X, Y)$。最开始时，$A$ 和 $B$ 均等于 $N$。 - 如果点位于纸张的边界或外部，即 $X \geq A$ 或 $Y \geq B$，那么该点将被忽略。 - 如果点在纸张内部，则需要在通过该点的一条横向直线和一条纵向直线之间选择一条来切割纸张。横向切割时保留上方部分，丢弃下方部分；纵向切割时保留左侧部分，丢弃右侧部分。在这两种情况下，选择保留下来的矩形面积较大的方式。如果两种方式得到的剩余矩形面积相同，则选择横向切割。 请考虑以下示例。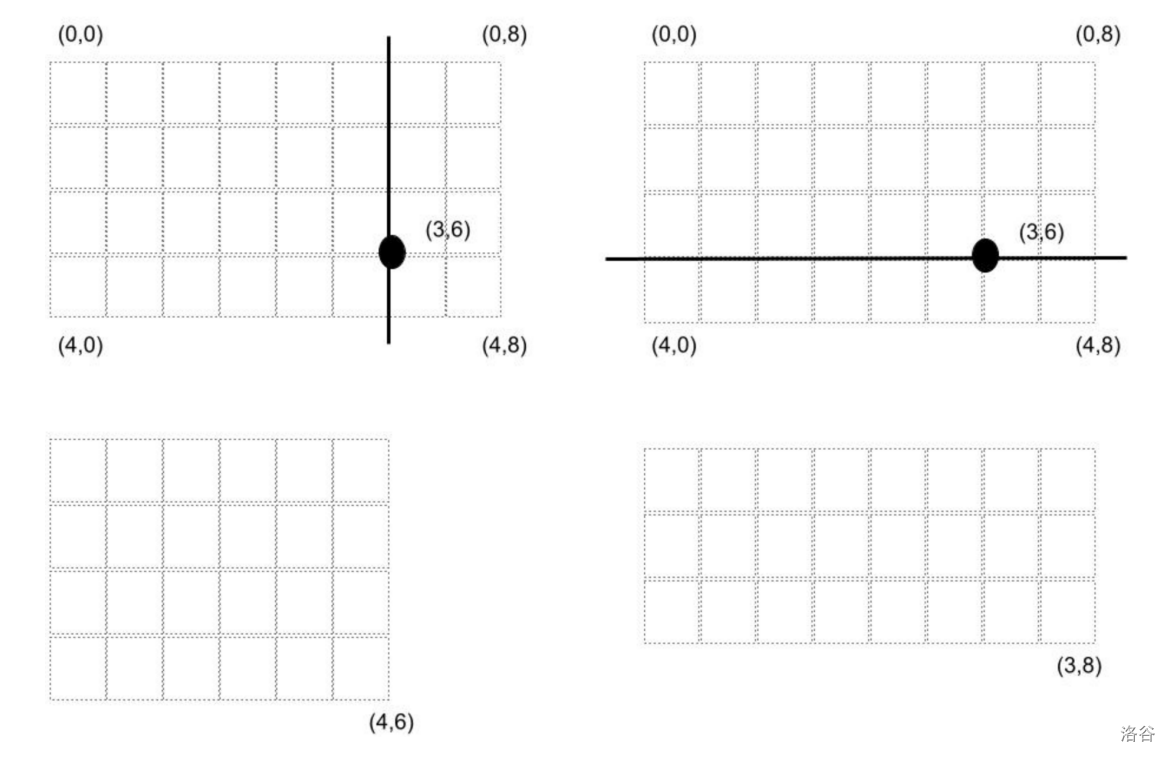  假设有一张竖直长度为 4、水平长度为 8 的纸张，考虑点 $(3, 6)$。图中的每个小格子面积为 1。在这种情况下，若以该点为基准进行纵向切割，则剩下竖直长度为 4、水平方向为 6 的纸张；若以该点为基准进行横向切割，则剩下竖直长度为 3、水平方向为 8 的纸张。两种纸张的面积均为 $24$，因此根据条件应选择横向切割。于是，该例中剩下的纸张为竖直长度为 3、水平方向为 8。 请计算依次对所有 $C$ 个点从第 1 个到第 $C$ 个执行上述操作后，最终剩下的纸张的面积。

第一行包含两个整数 $N$ 和 $C$，中间以一个空格分隔。接下来的 $C$ 行中，每行包含两个整数 $X$ 和 $Y$，表示一个点的坐标，按顺序给出，整数之间用一个空格分隔。

输出仅一行，表示最终剩下的纸张的面积。

**约束条件** - $1 \leq N \leq 10^4$ - $1 \leq C \leq 10^4$ - 所有给出的点 $(X, Y)$ 都满足 $1 \leq X, Y \leq N$ **子任务** 1. （5 分）数据为示例之一。 2. （15 分）$C = 1$ 3. （20 分）对于每个点，若不被忽略，则保证横向切割后保留下来的上方部分面积不小于纵向切割后保留下来的左侧部分面积。 4. （60 分）无额外约束条件。